题目内容
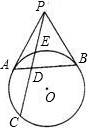 如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE=2,CD=1,求DE的长.
如图,PA、PB是⊙O的两条切线,PEC是一条割线,D是AB与PC的交点,若PE=2,CD=1,求DE的长.
分析:连接PO交AB于H,设DE=x,由勾股定理得,(x+2)2+x=2(x+3),从而求出x的值即可.
解答:解:连接PO交AB于H,由切线长定理可知,OP平分∠APB,而PA=PB,
∴PO⊥AB,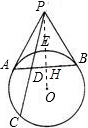
设DE=x,则PA2=PE•PC=2(x+3).
在Rt△APH中,AP2=AH2+PH2,即AH2+PH2=2(x+3)①,
在Rt△PHD中,PH2+DH2=(x+2)2②,
又AD•DB=ED•DC,而AD•DB=(AH-DH)(AH+DH)=AH2-DH2,
∴AH2-DH2=x•1③,
由①②③得(x+2)2+x=2(x+3),
解得DE=x=
.
∴PO⊥AB,

设DE=x,则PA2=PE•PC=2(x+3).
在Rt△APH中,AP2=AH2+PH2,即AH2+PH2=2(x+3)①,
在Rt△PHD中,PH2+DH2=(x+2)2②,
又AD•DB=ED•DC,而AD•DB=(AH-DH)(AH+DH)=AH2-DH2,
∴AH2-DH2=x•1③,
由①②③得(x+2)2+x=2(x+3),
解得DE=x=
| ||
| 2 |
点评:本题考查的是切割线定理,切线的性质定理,勾股定理.

练习册系列答案
相关题目
 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
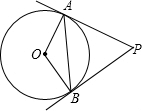 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
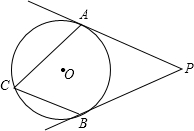
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于