题目内容
【题目】如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
(1)求证:CD是⊙M的切线;
(2)求线段ON的长.
【答案】
(1)
证明:OA、OB长是关于x的方程x2﹣mx+12=0的两实根,OA=4,则OA×OB=12,
得OB=3,⊙M的半径为1.5;
∵BM=CM=1.5,
∴∠OBA=∠BCM.
连结OC,OB是⊙M的直径,则∠ACO=90°,D为OA的中点,
∴OD=AD=CD=2,
∴∠OAC=∠ACD,
又∵∠OAC+∠OBA=90°,
∴∠BCM+∠ACD=90°,
∴∠NCD=90°,
∴CD是⊙M的切线.
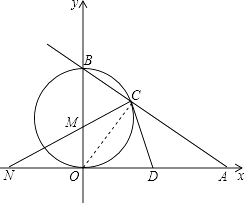
(2)
解:∵∠CND=∠CND,∠NOM=∠NCD=90°,
∴△NOM∽△NCD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴NO= ![]() .
.
【解析】(1)先根据根与系数的关系求出OB的长,故可得出圆的半径.连结OC,OB是⊙M的直径,则∠ACO=90°,由D为OA的中点得出OD=AD=CD,故可得出∠OAC=∠ACD,再由∠OAC+∠OBA=90°得出∠BCM+∠ACD=90°,故∠NCD=90°,由此得出结论;(2)根据∠CND=∠CND,∠NOM=∠NCD=90°,得出△NOM∽△NCD,再由相似三角形的对应边成比例即可得出结论.
【考点精析】关于本题考查的切线的性质定理,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

练习册系列答案
相关题目