Question

【题目】如图，已知矩形ABCD与矩形EFGO在平面直角坐标系中，点B的坐标为（﹣4，4），点F的坐标为（2，1），若矩形ABCD和矩形EFGO是位似图形，点P（点P在线段GC上）是位似中心，则点P的坐标为（ ）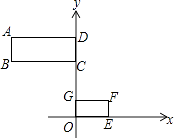

A.（0，3）
B.（0，2.5）
C.（0，2）
D.（0，1.5）

Answer 1

【答案】C
【解析】解：连接BF交y轴于点P，
∵点B的坐标为（﹣4，4），点F的坐标为（2，1），
∴BC=4，GF=2，CG=3，
∵BC∥GF，
∴△BCP∽△FGP，
∴ = ，即 = ，
解得，GP=1，
∴OP=2，
∴点P的坐标为（0，2），
故选：C．

【考点精析】通过灵活运用位似变换，掌握它们具有相似图形的性质外还有图形的位置关系（每组对应点所在的直线都经过同一个点—位似中心）即可以解答此题．