题目内容
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况.2019年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度(单位:微粒/立方米)表
浓度(单位:微粒/立方米)表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 33 | 海淀 | 50 | 平谷 | 45 |
密云 | 34 | 延庆 | 51 | 丰台 | 61 |
门头沟 | 41 | 西城 | 61 | 大兴 | 72 |
顺义 | 41 | 东城 | 60 | 开发区 | 65 |
昌平 | 38 | 石景山 | 55 | 房山 | 62 |
朝阳 | 54 | 通州 | 57 |
从上述表格随机选择一个区域,其2019年1月份![]() 的浓度小于51微克/立方米的概率是______.
的浓度小于51微克/立方米的概率是______.
【答案】![]()
【解析】
共有17个区域,![]() 的浓度小于51微克/立方米的有7个区域,利用概率公式可得答案.
的浓度小于51微克/立方米的有7个区域,利用概率公式可得答案.
解:∵共有17个区域,![]() 的浓度小于51微克/立方米的有7个区域,
的浓度小于51微克/立方米的有7个区域,
∴随机选择一个区域,其2019年1月份![]() 的浓度小于51微克/立方米的概率是
的浓度小于51微克/立方米的概率是![]() ,
,
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】在正方形ABCD中,AB=4cm,AC为对角线,AC上有一动点P,M是AB边的中点,连接PM、PB,设A、P两点间的距离为xcm,PM+PB长度为ycm.
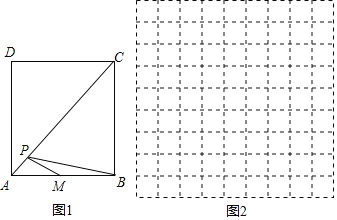
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 6.0 | 4.8 | 4.5 | 6.0 | 7.4 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:PM+PB的长度最小值约为______cm.
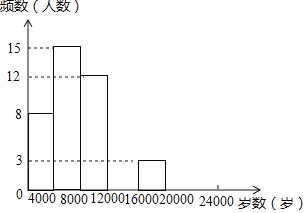
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.