Question

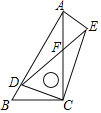
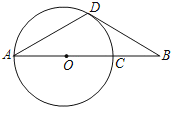
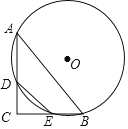
【题目】如图，在△ABC中，tan∠BACtan∠ABC=1，⊙O经过A、B两点，分别交AC、BC于D、E两点，若DE=10，AB=24，则⊙O的半径为____．

Answer 1

【答案】13．

【解析】

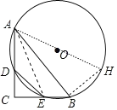
延长AO交⊙O于H，连接AE，BH．想办法证明∠CAE＝∠BAH，推出DE＝BH＝10，利用勾股定理求出AH即可解决问题．

延长AO交⊙O于H，连接AE，BH．

∵tan∠BACtan∠ABC=1，

∴∠BAC+∠ABC=90°，

∴∠C=90°，∴∠CAE+∠AEC=90°．

∵∠AEC+∠AEB=180°，∠AEB+∠H=180°，

∴∠AEC=∠H．

∵∠H+∠BAH=90°，

∴∠CAE=∠BAH，

∴，DE=BH=10．

∵AH是直径，∴∠ABH=90°，

∴AH26，

∴OA=OHAH=13．

故答案为：13．