题目内容
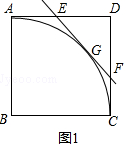
【题目】在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1 , 设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.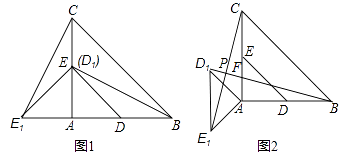
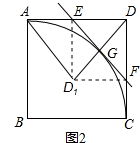
(1)如图1,当α=90°时,线段BD1的长等于 , 线段CE1的长等于;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1= CE1 , 且BD1⊥CE1;
(3)①设BC的中点为M,则线段PM的长为;②点P到AB所在直线的距离的最大值为 . (直接填写结果)
【答案】
(1)2 ![]() ;2
;2 ![]()
(2)
证明:当α=135°时,如图2,
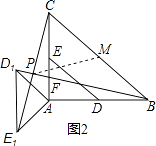
∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到,
∴AD1=AE1,∠D1AB=∠E1AC=135°,
在△D1AB和△E1AC中
∵ 
∴△D1AB≌△E1AC(SAS),
∴BD1=CE1,且∠D1BA=∠E1CA,
记直线BD1与AC交于点F,
∴∠BFA=∠CFP,
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1;
(3)2 ![]() ;1+
;1+ ![]()
【解析】解:(1)∵∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,
∴AE=AD=2,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1 , 设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=2,∠E1AE=90°,
∴BD1= ![]() =2
=2 ![]() ,E1C=
,E1C= ![]() =2
=2 ![]() ;
;
所以答案是:2 ![]() ,2
,2 ![]() ;
;
3)解:①如图2,
∵∠CPB=∠CAB=90°,BC的中点为M,
∴PM= ![]() BC,
BC,
∴PM= ![]() =2
=2 ![]() ,
,
所以答案是:2 ![]() ;
;
②如图3,作PG⊥AB,交AB所在直线于点G,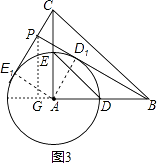
∵D1 , E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,则BD1= ![]() =2
=2 ![]() ,
,
故∠ABP=30°,
则PB=2+2 ![]() ,
,
故点P到AB所在直线的距离的最大值为:PG=1+ ![]() .
.
所以答案是:1+ ![]() .
.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.