题目内容
【题目】如图1所示,在正方形ABCD中,AB=1, ![]() 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作 ![]() 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点. 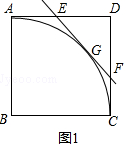
(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
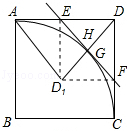
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1 , D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由. 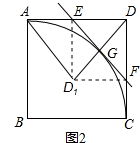
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,AD=CD=AB=1,
∴AD⊥BA,
∴AD是圆B的切线,
∵EG是圆B的切线,
∴EA=EG
(2)解:∵EF切圆B于点G,
∴EA=EG,FC=FG.
∵AE=x,FC=y
∴EF=x+y,DE=1﹣x,DF=1﹣y,
在Rt△DEF中,根据勾股定理,得:(x+y)2=(1﹣x)2+(1﹣y)2
∴y= ![]() (0<x<1)
(0<x<1)
(3)解:当点E运动到AD的中点时,△AD1D与△ED1F相似;理由如下:
设直线EF交线段DD1于点H,由题意,得:
△EDF≌△ED1F,EF⊥DD1且DH=D1H.
∵AE= ![]() ,AD=1,
,AD=1,
∴AE=ED.
∴EH∥AD1,∠AD1D=∠EHD=90°.
又∵∠ED1F=∠EDF=90°,
∴∠FD1D=∠AD1D.
∴D1F∥AD,
∴∠ADD1=∠DD1F=∠EFD=45°,
∴△ED1F∽△AD1D.
【解析】(1)证出AD是圆B的切线,由切线长定理即可得出结论;(2)根据切线长定理、正方形的性质得到有关的线段用x,y表示,再根据勾股定理建立函数关系式.(3)根据切线长定理找到角之间的关系,从而发现正方形,根据正方形的性质得到两个角对应相等,从而证明三角形相似.