题目内容
如图，AB是⊙O的直径，P在AB的延长线上，PD与⊙O相切于D，C在⊙O上，PC＝PD.
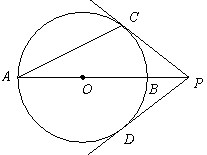
（1）求证：PC是⊙O的切线.
（2）连接AC，若AC＝PC，PB＝1，求⊙O的半径.
（1）求证：PC是⊙O的切线.
（2）连接AC，若AC＝PC，PB＝1，求⊙O的半径.
（1）连接OC、OD,在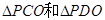
中，
，
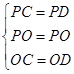所以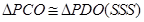
，
又因为PD是圆的切线，所以∠OCP＝90°，即PC是⊙O的切线.
（2）因为AC＝PC，
所以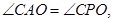
又因为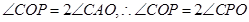
，
又因为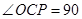
°，所以∠CPA＝30°，所以OP=2OC，因为PB＝1，所以r＝1.
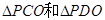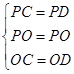中，，所以
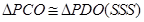，又因为PD是圆的切线，所以∠OCP＝90°，即PC是⊙O的切线.
（2）因为AC＝PC，
所以
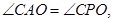又因为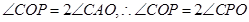，又因为
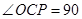°，所以∠CPA＝30°，所以OP=2OC，因为PB＝1，所以r＝1.（1）连接OC、OD，证明∠OCP＝90°；
（2）可证明∠COP＝2∠CAP＝2∠CPA，所以∠CPA＝30°，∴r＝1.
（2）可证明∠COP＝2∠CAP＝2∠CPA，所以∠CPA＝30°，∴r＝1.
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
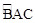的中点，连接PA、PB、PC、PD，当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并加以证明。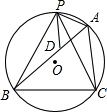
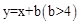与x轴、y轴分别相交于点A、B，与正比例函数
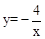的图象相交于点C、D（点C在点D的左侧），⊙O是以CD长为半径的圆。CE∥x轴，DE∥y轴，CE、DE相交于点E。
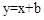与⊙O有哪些位置关系？求出相应b的取值范围。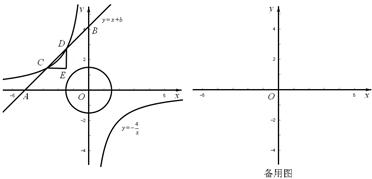
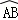所在圆的圆心为O′时，求O′A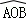的长度；
的长度；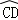
所在圆外切于点P时，设点O到弦AB．CD的距离之和为d，求d的值；
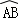与
所在圆外切于点P时，设点M为AB的中点，点N为CD的中点，试探究四边形OMPN的形状，并证明你的结论．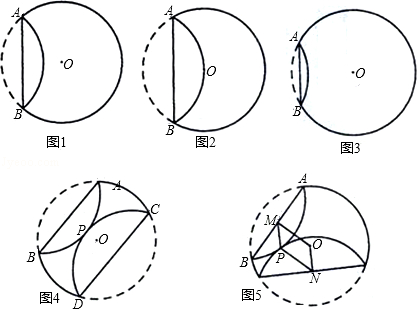
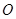为圆心，任意长为半径画弧，与射线
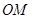交于点
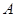，再以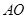
长为半径画弧，两弧交于点
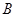，画射线
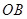，则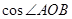
的值等于 ．
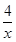上，以P为圆心的⊙P与两坐标轴都相切，E为y轴负半轴上的一点，PF⊥PE交x轴于点F，则OF－OE的值是 ___________．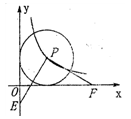
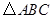中，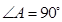
，
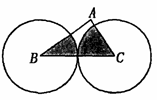
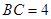cm，分别以B、C为圆心的两个等圆外切，则图中阴影部分的面积为 
．
、
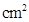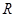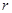分别为方程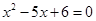
的两根，两圆的圆心距为1，两圆的位置关系是 ．