题目内容
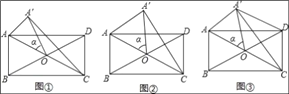
【题目】在矩形ABCD中,AB=1,BC=2,对角线AC、BD相交于点O,点A绕点O按顺时针方向旋转到A′,旋转角为α(0°<α<∠AOD),连接A′C.
(1)如图①,则△AA′C的形状是 ;
(2)如图②,当∠α=60°,求A′C长度;
(3)如图③,当∠α=∠AOB时,求证:A′D∥AC.
【答案】(1)直角三角形;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:
(1)由题意易得:A′O=AO=BO,由此可得∠OAA′=∠OA′A,∠OA′C=∠OCA′,结合三角形内角和为180°即可得到∠AA′C=90°,从而可得△A′AC是直角三角形;
(2)由已知条件易得:AC=![]() ,则由矩形的性质可得OA=OA′=
,则由矩形的性质可得OA=OA′=![]() ,结合∠α=60°,
,结合∠α=60°,
可得△AA′O是等边三角形,从而可得∠OAA′=60°,结合∠AA′C=90°,可得A′C=sin∠OAA′×AC=![]() ;
;
(3)由题意易得OD=OA=OA′,由此可得∠OA′D=∠ODA′,则可得∠OA′D=![]() (180°-∠DOA′);由∠α=∠AOB,∠α+∠AOB+∠DOA′=180°可得∠α=
(180°-∠DOA′);由∠α=∠AOB,∠α+∠AOB+∠DOA′=180°可得∠α=![]() (180°-∠∠DOA′);由此即可得到∠α=∠OA′D,从而可得A′D∥AC.
(180°-∠∠DOA′);由此即可得到∠α=∠OA′D,从而可得A′D∥AC.
试题解析:
(1)∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵OA=OA′,
∴OA′=OC,
∴∠OAA′=∠OA′A,∠OA′C=∠OCA′,
∴∠OA′C+∠OA′A=∠OCA′+∠OAA′,
∴∠CA′A=90°,
∴△AA′C是直角三角形,
故答案为:直角三角形;
(2)∵AB=1,BC=2,
∴AC![]() ,
,
∴OA=OA′=![]() ,
,
∵∠α=60°,
∴△AA′O是等边三角形,
∴∠OAA′=60°,
∴A′C=![]() AC=
AC=![]() ;
;
(3)∵∠α=∠AOB,∠α+∠AOB+∠DOA′=180°,
∴∠α=![]() (180°-∠∠DOA′),
(180°-∠∠DOA′),
∵四边形ABCD是矩形,OA′是由OA绕点O旋转得到的,
∴OD=OA=OA′,
∴∠OA′D=∠ODA′,
∴∠OA′D=![]() (180°-∠DOA′),
(180°-∠DOA′),
∴∠α=∠OA′D,
∴A′D∥AC.

【题目】全民健身运动已成为一种时尚 ,为了解揭阳市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷内容包括五个项目:
A:健身房运动;B:跳广场舞;C:参加暴走团;D:散步;E:不运动.
以下是根据调查结果绘制的统计图表的一部分,
运动形式 | A | B | C | D | E |
人数 |
|
|
|
|
|
请你根据以上信息,回答下列问题:
![]() 接受问卷调查的共有 人,图表中的
接受问卷调查的共有 人,图表中的![]() ,
,![]() .
.
![]() 统计图中,
统计图中,![]() 类所对应的扇形的圆心角的度数是 度.
类所对应的扇形的圆心角的度数是 度.

![]() 揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有
揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有![]() 人,请你估计一下该社区参加环岛路“暴走团”的人数.
人,请你估计一下该社区参加环岛路“暴走团”的人数.