题目内容
 已知:如图,四边形OABC是菱形,点C在x轴上,点A在直线y=x上,B点在反比例函数y=
已知:如图,四边形OABC是菱形,点C在x轴上,点A在直线y=x上,B点在反比例函数y=| k |
| x |
| 2 |
分析:首先根据直线y=x经过点A,设A点坐标为(a,a),再利用勾股定理算出AO=
a,进而得到AO=CO=CB=AB=
a,再利用菱形的面积公式计算出a的值,进而得到A点坐标,进而得到B点坐标,再利用待定系数法求出反比例函数表达式.
| 2 |
| 2 |
解答:解:∵直线y=x经过点A,
∴设A(a,a),
∴OA2=2a2,
∴AO=
a,
∵四边形ABCD是菱形,
∴AO=CO=CB=AB=
a,
∵菱形OABC的面积是
,
∴
a•a=
,
∴a=1,
∴AB=
,A(1,1)
∴B(1+
,1),
设反比例函数解析式为y=
(k≠0),
∵B(1+
,1)在反比例函数图象上,
∴k=(1+
)×1=
+1,
∴反比例函数解析式为y=
.
故选C.
∴设A(a,a),
∴OA2=2a2,
∴AO=
| 2 |
∵四边形ABCD是菱形,
∴AO=CO=CB=AB=
| 2 |
∵菱形OABC的面积是
| 2 |
∴
| 2 |
| 2 |
∴a=1,
∴AB=
| 2 |
∴B(1+
| 2 |
设反比例函数解析式为y=
| k |
| x |
∵B(1+
| 2 |
∴k=(1+
| 2 |
| 2 |
∴反比例函数解析式为y=
| ||
| x |
故选C.
点评:此题主要考查了待定系数法求反比例函数,菱形的面积公式,菱形的性质,关键是根据菱形的面积求出A点坐标,进而得到B点坐标,即可算出反比例函数解析式.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
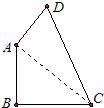 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.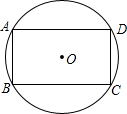 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.