题目内容
已知：如图，四边形ABCD中，BC=CD=10，AB=15，AB⊥BC，CD⊥BC，若把四边形ABCD绕直线AB旋转一周，则所得几何体的表面积是多少？分析：首先判断该四边形经过旋转后得到的几何体的形状，然后求其表面积即可．
解答：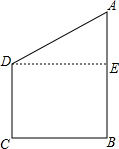
解：作DE⊥AB于点E，
把四边形ABCD绕直线AB旋转一周形成一个下面是圆柱，上面是圆锥的几何图形，
圆柱的高CD=10，底面半径BC=10，圆锥的母线长AD=
=
=5
∴该几何体的表面积为πRl+2πRh+πrR2=π×10×5
+2π×10×10+π×100=（300+50
）π
解：作DE⊥AB于点E，把四边形ABCD绕直线AB旋转一周形成一个下面是圆柱，上面是圆锥的几何图形，
圆柱的高CD=10，底面半径BC=10，圆锥的母线长AD=
| AE2+DE2 |
| 102+52 |
| 5 |
∴该几何体的表面积为πRl+2πRh+πrR2=π×10×5
| 5 |
| 5 |
点评：本题考查了圆锥的计算，解题的关键是了解该四边形经过旋转后得到的几何体的形状．
练习册系列答案
相关题目
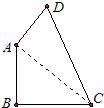已知，如图，四边形ABCD中∠B=90°，AB=9，BC=12，AD=8，CD=17．
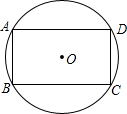已知：如图，四边形ABCD内接于⊙O，且AB∥CD，AD∥BC，
已知，如图，四边形ABCD是正方形，E、F分别是AB和AD延长线上的点，且BE=DF
已知：如图，四边形ABCD及一点P．