Question

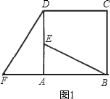
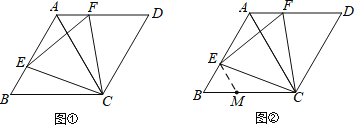
【题目】已知，如图，在△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线交AD于E，交AC于F，∠CAD的角平分线AG交BF于H，交DC于G．

（1）求证：AE=AF；

（2）判断BF与AG的位置关系，并说明理由．

（3）再找出二组相等的线段：① ； ② ．

Answer 1

【答案】（1）见解析；（2）BF⊥AG，理由见解析；（3）EH=FH，BA=BG

【解析】

（1）根据等角的余角相等，得到∠AFB=∠BED，则∠AFB=∠AEF，即可得到AE=AF；

（2）由AE=AF，AG平分∠CAD，由三线合一定理，得到AH是等腰三角形AEF的高，即BF⊥AG；

（3）由（2）知△AEF是等腰三角形，则EH=FH，由BH是△ABG的边AG上的高，也是角平分线，则BA=BG.

解：（1）∵∠BAC=90°，AD⊥BC于D，

∴∠ABF+∠AFB=∠CBF+∠BED=90°，

∵BF平分∠ABC，

∴∠ABF=∠CBF，

∴∠AFB=∠BED，

∵∠BED=∠AEF，

∴∠AFB=∠AEF，

∴AE=AF；

（2）在△AEF中，AE=AF，

∵AG平分∠CAD，

即AH平分∠FAE，

∴AH是等腰三角形AEF的高，

∴BF⊥AG；

（3）由（2）知，△AEF是等腰三角形，

∵AH⊥EF，

∴EH=FH，

∵BF⊥AG，BF平分∠ABC，

∴△ABG是等腰三角形，

∴AB=BG.

故答案为：EH=FH，AB=BG.