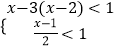��Ŀ����
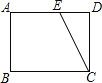
����Ŀ��ͼ1��ͼ2�е�������ABCD���ı���AEFG���������Σ� 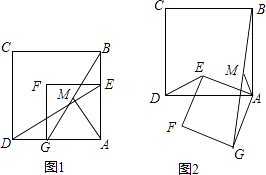
��1����ͼ1������DE��BG��MΪ�߶�BG���е㣬����AM��̽��AM��DE��������ϵ��λ�ù�ϵ����֤����Ľ��ۣ�
��2����ͼ1�Ļ����ϣ���������AEFG�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�����DE��BG��MΪ�߶�BG���е㣬����AM��̽��AM��DE��������ϵ��λ�ù�ϵ����֤����Ľ��ۣ�
���𰸡�
��1���⣺AM= ![]() DE��AM��DE�������ǣ�
DE��AM��DE�������ǣ�
��ͼ1����AM��DE�ڵ�O��
���ı���ABCD���ı���AEFG���������Σ�
��AG=AE��AD=AB��
�ߡ�DAE=��BAG��
���DAE�ա�BAG��
��DE=BG����AED=��AGB��
��Rt��ABG��
��MΪ�߶�BG���е㣬
��AM= ![]() BG��AM=BM��
BG��AM=BM��
��AM= ![]() DE��
DE��
��AM=BM��
���MBA=��MAB��
�ߡ�AGB+��MBA=90�㣬
���MAB+��AED=90�㣬
���AOE=90�㣬��AM��DE
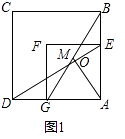
��2���⣺AM= ![]() DE��AM��DE�������ǣ�
DE��AM��DE�������ǣ�
��ͼ2���ӳ�AM��N��ʹMN=AM������NG��
��MN=AM��MG=BM����NMG=��BMA��
���MNG�ա�MAB��
��NG=AB����N=��BAN��
�ɣ�1���ã�AB=AD��
��NG=AD��
�ߡ�BAN+��DAN=90�㣬
���N+��DAN=90�㣬
��NG��AD��
���AGN+��DAG=90�㣬
�ߡ�DAG+��DAE=��EAG=90�㣬
���AGN=��DAE��
��NG=AD��AG=AE��
���AGN�ա�EAD��
��AN=DE����N=��ADE��
�ߡ�N+��DAN=90�㣬
���ADE+��DAN=90�㣬
��AM��DE��
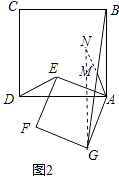
����������1��AM= ![]() DE��AM��DE�������ǣ���֤����DAE�ա�BAG����DE=BG����AED=��AGB���ٸ���ֱ��������б�ߵ����ߵ����ʵ�AM=
DE��AM��DE�������ǣ���֤����DAE�ա�BAG����DE=BG����AED=��AGB���ٸ���ֱ��������б�ߵ����ߵ����ʵ�AM= ![]() BG��AM=BM����AM=
BG��AM=BM����AM= ![]() DE���ɽǵĹ�ϵ�á�MAB+��AED=90�㣬���ԡ�AOE=90�㣬��AM��DE����2��AM=
DE���ɽǵĹ�ϵ�á�MAB+��AED=90�㣬���ԡ�AOE=90�㣬��AM��DE����2��AM= ![]() DE��AM��DE�������ǣ��������߹���ȫ�������Σ�֤����MNG�ա�MAB�͡�AGN�ա�EAD���Եó����ۣ�
DE��AM��DE�������ǣ��������߹���ȫ�������Σ�֤����MNG�ա�MAB�͡�AGN�ա�EAD���Եó����ۣ�