题目内容
如图所示,⊙O的直径AB=2,AD,BC是它的两条切线,且CD与⊙O相切于点E,交AD,BC于 点D,C,设AD=x,BC=y.
点D,C,设AD=x,BC=y.(1)求证:AD+BC=CD;
(2)求y关于x的函数关系,并画去它的图象;
(3)若x,y是方程2t2-5t+m=0的两根,求x,y的值;
(4)求四边形的ABCD的面积S,(用字母表示)并证明S≥2.
分析:(1)首先连接OE,由AD,BC是它的两条切线,CD与⊙O相切于点E,根据切线长定理,即可得AD=DE,EC=BC,又由CD=DE+CE,即可证得AD+BC=CD;
(2)过点D作DM⊥BC于M,由AD,BC是它的两条切线,可得AB⊥AD,AB⊥BC,即可证得四边形ABMD是矩形,则可求得DM与CM的长,由勾股定理,即可得方程(x+y)2=4+(y-x)2,解此方程组即可求得y关于x的函数关系;
(3)由x,y是方程2t2-5t+m=0的两根,根据根与系数的关系求得m的值,然后解方程即可求得x,y的值;
(4)根据(3)可得四边形ABCD是梯形,根据梯形面积的求解方法,可得S=xy,又由y=
,根据几何不等式的性质,即可证得S≥2.
(2)过点D作DM⊥BC于M,由AD,BC是它的两条切线,可得AB⊥AD,AB⊥BC,即可证得四边形ABMD是矩形,则可求得DM与CM的长,由勾股定理,即可得方程(x+y)2=4+(y-x)2,解此方程组即可求得y关于x的函数关系;
(3)由x,y是方程2t2-5t+m=0的两根,根据根与系数的关系求得m的值,然后解方程即可求得x,y的值;
(4)根据(3)可得四边形ABCD是梯形,根据梯形面积的求解方法,可得S=xy,又由y=
| 1 |
| x |
解答: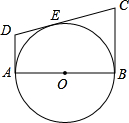 (1)证明:连接OE,
(1)证明:连接OE,
∵AD,BC是它的两条切线,CD与⊙O相切于点E,
∴AD=DE,EC=BC,
∴CD=DE+EC=AD+BC,
即:AD+BC=CD;
(2)解:过点D作DM⊥BC于M,
∵AD,BC是它的两条切线,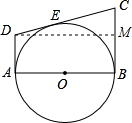
∴AB⊥AD,AB⊥BC,
∴∠A=∠B=∠BMD=90°
∴四边形ABMD是矩形,
∴DM=AB=2,BM=AD=x,
∴CD=AD+BC=x+y,CM=BC-BM=y-x,
∵CD2=DM2+CM2,
∴(x+y)2=4+(y-x)2,
即:y=
,
∴y关于x的函数关系为:y=
,
它的图象为:
(3)∵x,y是方程2t2-5t+m=0的两根,由根与系数的关系得:
∴xy=
=1,
解得:m=2,
∴原方程为:2t2-5t+2=0
∴(2t-1)(t-2)=0,
解得:t=
或t=2,
∴x=
,y=2;
(4)∵AD∥BC,
∴四边形ABCD是梯形,
∴S梯形ABCD=
(AD+BC)•DM=
(x+y)•2=x+y,
∵y=
,
∴S=x+y=x+
≥2
=2,
∴S≥2.
 (1)证明:连接OE,
(1)证明:连接OE,∵AD,BC是它的两条切线,CD与⊙O相切于点E,
∴AD=DE,EC=BC,
∴CD=DE+EC=AD+BC,
即:AD+BC=CD;
(2)解:过点D作DM⊥BC于M,
∵AD,BC是它的两条切线,

∴AB⊥AD,AB⊥BC,
∴∠A=∠B=∠BMD=90°
∴四边形ABMD是矩形,
∴DM=AB=2,BM=AD=x,
∴CD=AD+BC=x+y,CM=BC-BM=y-x,
∵CD2=DM2+CM2,

∴(x+y)2=4+(y-x)2,
即:y=
| 1 |
| x |
∴y关于x的函数关系为:y=
| 1 |
| x |
它的图象为:
(3)∵x,y是方程2t2-5t+m=0的两根,由根与系数的关系得:
∴xy=
| m |
| 2 |
解得:m=2,
∴原方程为:2t2-5t+2=0
∴(2t-1)(t-2)=0,
解得:t=
| 1 |
| 2 |
∴x=
| 1 |
| 2 |
(4)∵AD∥BC,
∴四边形ABCD是梯形,
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∵y=
| 1 |
| x |
∴S=x+y=x+
| 1 |
| x |
x•
|
∴S≥2.
点评:此题考查了切线的性质,梯形的性质,矩形的判定与性质,勾股定理,反比例函数的性质以及几何不等式的应用.此题综合性较强,难度较大,解题的关键是注意数形结合思想与方程思想的应用,注意辅助线的作法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 为C,连接AC.
为C,连接AC.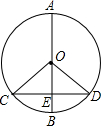 如图所示,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE,∠D的度数.
如图所示,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE,∠D的度数.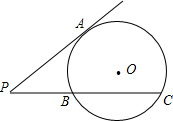 如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根. P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根. P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值. 如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求圆心O到CD的距离.
如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求圆心O到CD的距离.