题目内容
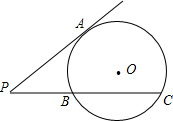 如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根. P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根. P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
分析:设方程x2+2(k-2)x+k=0的两个根为x1,x2,x1≤x2,x1,x2都是整数,因为BC=PC-PB为正整数,所以BC=1,2,3或4,讨论BC的值即可求得PA2+PB2+PC2的值,即可解题.
解答: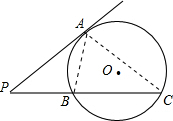 解:
解:
设方程x2+2(k-2)x+k=0的两个根
为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
由题设及①知,x1,x2都是整数.从①,②消去k,得2x1x2+x1+x2=4,(2x1+1)(2x2+1)=9.
由上式知,x2≤4,且当k=0时,x2=4,故最大的整数根为4.
于是⊙O的直径为4,所以BC≤4.
因为BC=PC-PB为正整数,所以BC=1,2,3或4.
连接AB,AC,因为∠PAB=∠PCA,所以△PAB∽△PCA,
=
.
故PA2=PB(PB+BC)③
(1)当BC=1时,由③得,PA2=PB2+PB,于是PB2<PA2<(PB+1)2,矛盾!
(2)当BC=2时,由③得,PA2=PB2+2PB,于是PB2<PA2<(PB+1)2,矛盾!
(3)当BC=3时,由③得,PA2=PB2+3PB,于是(PA-PB)(PA+PB)=3PB,
由于PB不是合数,结合PA-PB<PA+PB,
故只可能
,
,
,
解得
此时PA2+PB2+PC2=21.
(4)当BC=4,由③得,PA2=PB2+4PB,于是(PB+1)2<PB2+4PB=PA2<(PB+2)2,矛盾.
综上所述PA2+PB2+PC2=21.
 解:
解:设方程x2+2(k-2)x+k=0的两个根
为x1,x2,x1≤x2.由根与系数的关系得x1+x2=4-2k,①x1x2=k.②
由题设及①知,x1,x2都是整数.从①,②消去k,得2x1x2+x1+x2=4,(2x1+1)(2x2+1)=9.
由上式知,x2≤4,且当k=0时,x2=4,故最大的整数根为4.
于是⊙O的直径为4,所以BC≤4.
因为BC=PC-PB为正整数,所以BC=1,2,3或4.
连接AB,AC,因为∠PAB=∠PCA,所以△PAB∽△PCA,
| PA |
| PB |
| PC |
| PA |
故PA2=PB(PB+BC)③
(1)当BC=1时,由③得,PA2=PB2+PB,于是PB2<PA2<(PB+1)2,矛盾!
(2)当BC=2时,由③得,PA2=PB2+2PB,于是PB2<PA2<(PB+1)2,矛盾!
(3)当BC=3时,由③得,PA2=PB2+3PB,于是(PA-PB)(PA+PB)=3PB,
由于PB不是合数,结合PA-PB<PA+PB,
故只可能
|
|
|
解得
|
此时PA2+PB2+PC2=21.
(4)当BC=4,由③得,PA2=PB2+4PB,于是(PB+1)2<PB2+4PB=PA2<(PB+2)2,矛盾.
综上所述PA2+PB2+PC2=21.
点评:本题考查了一元二次方程的求解,考查了分类讨论思想,本题中讨论BC的值并求PA2+PB2+PC2是解题的关键.

练习册系列答案
相关题目
 为C,连接AC.
为C,连接AC. 点D,C,设AD=x,BC=y.
点D,C,设AD=x,BC=y.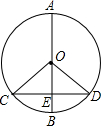 如图所示,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE,∠D的度数.
如图所示,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE,∠D的度数. 如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求圆心O到CD的距离.
如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求圆心O到CD的距离.