题目内容
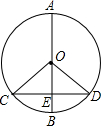 如图所示,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE,∠D的度数.
如图所示,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE,∠D的度数.
分析:在等腰△OCD中,OE⊥CD,根据等腰三角形三线合一的性质可知:OE必为顶角∠COD的角平分线;则∠EOD=∠COE=50°;进而可在Rt△OED中,求出∠D的度数.
解答:解:在△OCD中,OC=OD,OE⊥CD,
∴OE平分∠COD,又∠COD=100°,
∴∠COE=∠DOE=
∠COD=50°,
则在Rt△OED中,∠D=90°-∠DOE=90°-50°=40°.
∴OE平分∠COD,又∠COD=100°,
∴∠COE=∠DOE=
| 1 |
| 2 |
则在Rt△OED中,∠D=90°-∠DOE=90°-50°=40°.
点评:本题考查的直角三角形的性质以及等腰三角形的性质:等腰三角形中,底边上的高线、底边上的中线、顶角平分线互相重合.

练习册系列答案
相关题目
 为C,连接AC.
为C,连接AC. 点D,C,设AD=x,BC=y.
点D,C,设AD=x,BC=y.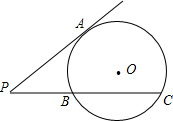 如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根. P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根. P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值. 如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求圆心O到CD的距离.
如图所示,⊙O的直径AB和弦CD交于E,已知AE=6cm,EB=2cm,∠CEA=30°,求圆心O到CD的距离.