题目内容
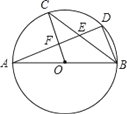
【题目】如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD
(1)求证:∠C=∠D;
(2)若⊙O的半径为r,请直接写出CE+ED的变化范围.
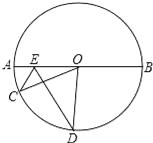
【答案】(1)证明见解析;(2)r<CE+ED<2r
【解析】
(1)延长CE交⊙O于D′,连接OD′,由已知求得∠AEC=60°,进而求得∠DEO=∠D′EO=60°,根据圆是轴对称图形即可证得∠D=∠D′,ED=ED′,然后根据等腰三角形的性质求得∠D′=∠C,从而证得结论;
(2)证得∠COD′>60°,从而证得CD′>OC=OD′,由CD′<OC+OD′,CE+ED=CE+ED′=CD′,从而得出r<CE+ED<2r.
证明:(1)延长CE交⊙O于D′,连接OD′
∵∠CED=∠OED=60°,
∴∠AEC=60°,
∴∠OED′=60°,
∴∠DEO=∠D′EO=60°,
由轴对称的性质可得∠D=∠D′,ED=ED′,
∵OC=OD′,
∴∠D′=∠C,
∴∠C=∠D;
(2)∵∠D′EO=60°,
∴∠C<60°,
∴∠C=∠D′<60°,
∴∠COD′>60°,
∴CD′>OC=OD′,
∵CD′<OC+OD′,
∵CE+ED=CE+ED′=CD′,
∴r<CE+ED<2r.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目