题目内容
【题目】如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=12,BC=18.
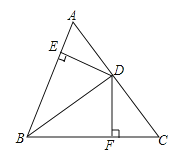
(1)求S△ABD∶S△BCD的值;
(2)若S△ABC=36,求DE的长.
【答案】(1)S△ABD∶S△BCD =2∶3;(2)DE=2.4.
【解析】
(1)根据角平分线的性质得到DE=DF,根据三角形的面积公式计算即可得到答案;
(2)根据三角形的面积公式计算即可求出DE的长.
解:(1)∵ BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,
∴ DE=DF
又 ∵ AB=12,BC=18
∴ S△ABD∶S△BCD=![]() AB·DE∶
AB·DE∶![]() BC·DF=2∶3
BC·DF=2∶3
(2)由题意得:![]() AB·DE+
AB·DE+![]() BC·DF=36
BC·DF=36
∴![]() ×12·DE+
×12·DE+![]() ×18·DE = 36
×18·DE = 36
解得:DE=2.4

练习册系列答案
相关题目