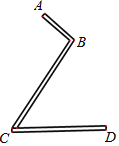
题目内容
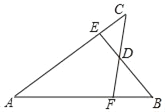
【题目】现有一个“![]() ”型的工件(工件厚度忽略不计),如图示,其中
”型的工件(工件厚度忽略不计),如图示,其中![]() 为20
为20![]() ,
,![]() 为60
为60![]() ,
,![]() ,
,![]() ,求该工件如图摆放时的高度(即
,求该工件如图摆放时的高度(即![]() 到
到![]() 的距离).
的距离).
(结果精确到0.1![]() ,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
【答案】58.8cm
【解析】
过B作BE⊥CD,垂足为E,过A作AF⊥BE,垂足为F,根据Rt△BCE的三角函数得出BE的长度,然后根据Rt△ABF的三角形你是得出BF的长度,最后根据EF=BE+BF得出答案.
过B作BE⊥CD,垂足为E,过A作AF⊥BE,垂足为F,
在Rt△BCE中, ∵sin∠BCE =![]() , ∴BE=BC·sin∠BCE≈60×0.766 ≈45.96
, ∴BE=BC·sin∠BCE≈60×0.766 ≈45.96
又∵∠ABC=90°∴∠ABF=50°;在Rt△ABF中cos∠ABF =![]()
∴BF=AB·cos∠ABF≈20×0.463 ≈12.86
∴EF=BE+BF=45.96+12.86=58.82≈58.8(cm).
答:工件摆放时的高度是58.8cm

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】下表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | -1 | - | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | 2 |
| -1 | - | -2 | - | -1 |
| 2 | … |
(1)此二次函数图象的顶点坐标是 ;
(2)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 。