题目内容
如图，已知⊙O中，弦AC、BD相交于点P，AB=5，AP=3，DP=2，则CD=| 10 |
| 3 |
| 10 |
| 3 |
分析：利用“角角相等”证得△ABP∽△CDP；然后根据相似三角形的对应边成比例列出比例式
=
；最后将已知线段的长度代入该比例式即可求得线段CD的长度．
| AB |
| DC |
| AP |
| DP |
解答：解：∵∠ABD=∠ACD（同弧所对的圆周角相等），∠APB=∠CPD（对顶角相等），
∴△ABP∽△DCP，
∴
=
，
又AB=5，AP=3，DP=2，
∴
=
，
解得DC=
，即CD=
．
故答案是：
．
解：∵∠ABD=∠ACD（同弧所对的圆周角相等），∠APB=∠CPD（对顶角相等），∴△ABP∽△DCP，
∴
| AB |
| DC |
| AP |
| DP |
又AB=5，AP=3，DP=2，
∴
| 5 |
| DC |
| 3 |
| 2 |
解得DC=
| 10 |
| 3 |
| 10 |
| 3 |
故答案是：
| 10 |
| 3 |
点评：本题考查了相似三角形的判定与性质．在证明△ABP与△CDP相似时，也可以不利用“对顶角相等”这一条件，直接利用圆周角定理推知：∠ABD=∠ACD，∠A=∠D．
练习册系列答案
相关题目
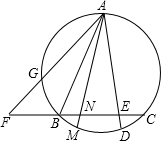如图，已知⊙O中，弦BC=8，A是
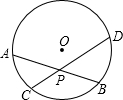如图，已知⊙O中，弦AB与CD相交于点P．
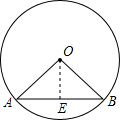如图，已知⊙O中，弦AB=12cm，O点到AB的距离等于AB的一半，则∠AOB的度数为