题目内容
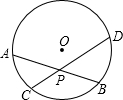如图，已知⊙O中，弦AB与CD相交于点P．求证：PA•PB=PC•PD．
分析：连接AC、DB，根据同弧所对的圆周角相等，证出△ACP∽△DBP，然后根据相似三角形的性质得出结论．
解答：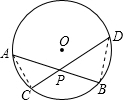
解：连接AC、BD．
∵∠A=∠D，∠C=∠B，
∴△ACP∽△DBP，
∴
=
，
∴PA•PB=PC•PD．
解：连接AC、BD．∵∠A=∠D，∠C=∠B，
∴△ACP∽△DBP，
∴
| PA |
| PD |
| PC |
| PB |
∴PA•PB=PC•PD．
点评：此题是通过相似三角形的性质来证明相交弦定理，关键是根据圆周角定理求出相等的角．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
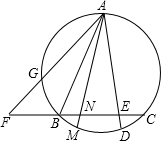如图，已知⊙O中，弦BC=8，A是
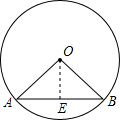如图，已知⊙O中，弦AB=12cm，O点到AB的距离等于AB的一半，则∠AOB的度数为
如图，已知⊙O中，弦AC、BD相交于点P，AB=5，AP=3，DP=2，则CD=