题目内容
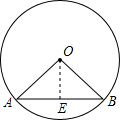 如图,已知⊙O中,弦AB=12cm,O点到AB的距离等于AB的一半,则∠AOB的度数为
如图,已知⊙O中,弦AB=12cm,O点到AB的距离等于AB的一半,则∠AOB的度数为分析:由O点到AB的距离等于AB的一半,得∠A=∠AOE=45°,则∠AOB=90°,再由勾股定理求得圆的半径.
解答:解:∵OE=AE,
∴∠A=∠AOE=45°,
同理得,∠B=∠BOE=45°,
∴∠AOB=90°,
∵AB=12cm,
∴OE=AE=6cm,
∴由勾股定理得,OA=
=6
cm.
故答案为:90,6
.
∴∠A=∠AOE=45°,
同理得,∠B=∠BOE=45°,
∴∠AOB=90°,
∵AB=12cm,
∴OE=AE=6cm,
∴由勾股定理得,OA=
| 62+62 |
| 2 |
故答案为:90,6
| 2 |
点评:本题考查了垂径定理和勾股定理,解此类题目要注意将圆的问题转化成三角形的问题再进行计算.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
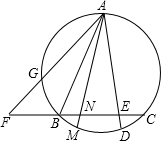 如图,已知⊙O中,弦BC=8,A是
如图,已知⊙O中,弦BC=8,A是
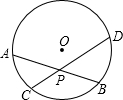 如图,已知⊙O中,弦AB与CD相交于点P.
如图,已知⊙O中,弦AB与CD相交于点P. 如图,已知⊙O中,弦AC、BD相交于点P,AB=5,AP=3,DP=2,则CD=
如图,已知⊙O中,弦AC、BD相交于点P,AB=5,AP=3,DP=2,则CD=