题目内容
【题目】菱形![]() 中,
中,![]() 为边
为边![]() 上的点,
上的点,![]() 相交于点
相交于点![]() .
.
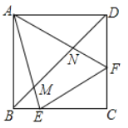
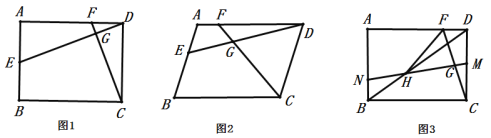
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() .求证:
.求证:![]() ;
;
(3)如图3,在(1)的条件下,平移线段![]() 到
到![]() ,使
,使![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
【答案】(1)见解析;(2)见解析;(3)1+![]() .
.
【解析】
(1)由菱形ABCD中和∠A=90°可得菱形ABCD是正方形,根据正方形性质得AD=DC,∠A=∠CDF=90°,再加上DE=CF即证得Rt△ADE≌Rt△DCF,所以∠ADE=∠DCF,等量代换计算即得到∠CGD=90°,得证.
(2)由菱形性质可得AD=CD,∠B=∠ADC,∠B+∠BAD=180°,再由∠EGC+∠B=180°可得∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC,证明△ADE∽△GDF和△DCG∽△FCD,再由对应边成比例等量代换计算得DE=CF.
(3)由(1)的条件可得MN=CF,MN⊥CF,加上G为CF的中点,即MN垂直平分CF,连接FM即有FM=MC且∠DMF=∠MFC+∠FCD=30°,设DF=x,则根据30°直角三角形的性质,可用x表示FM、DM.过点N作CD的垂线段NP,则CP=BN=![]() ,且易证Rt△NPM≌Rt△CDF,所以MP=DF=x,进而能用x表示CM、CD.利用MF=MC列出关于x的方程,求解即得到CM、CD、DF的长.证明△CGM∽△CDF,根据对应边成比例计算即求得FG=CG的长.
,且易证Rt△NPM≌Rt△CDF,所以MP=DF=x,进而能用x表示CM、CD.利用MF=MC列出关于x的方程,求解即得到CM、CD、DF的长.证明△CGM∽△CDF,根据对应边成比例计算即求得FG=CG的长.
解:(1)证明:∵菱形ABCD中,∠A=90°
∴菱形ABCD是正方形
∴AD=DC,∠A=∠CDF=90°
在Rt△ADE与Rt△DCF中
DE=CF,AD=DC,
∴Rt△ADE≌Rt△DCF(HL)
∴∠ADE=∠DCF
∴∠DCF+∠CDE=∠ADE+∠CDE=∠ADC=90°
∴∠CGD=90°
∴DE⊥CF
(2)证明:∵四边形ABCD是菱形
∴AD=CD,∠B=∠ADC,AD∥BC
∴∠A+∠B=180°
∵∠EGC+∠B=180°,∠EGC+∠CGD=180°
∴∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC
∵∠A=∠DGF,∠ADE=∠GDF
∴△ADE∽△GDF
∴![]() ,
,
∴![]()
∵∠CGD=∠CDF,∠DCG=∠FCD
∴△DCG∽△FCD
∴![]() ,
,
∴![]() ,
,
∵AD=DC,
∴DE=CF;
(3)如图,过点N作NP⊥CD于点P,连接FM,
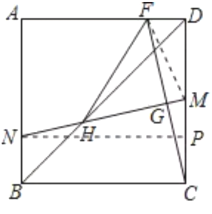
∴∠CPN=∠MPN=90°,
∵四边形ABCD是正方形
∴∠ABC=∠BCD=∠ADC=90°,BC=CD
∴四边形BCPN是矩形
∴NP=BC=CD,PC=BN=![]() ,
,
在Rt△NPM与Rt△CDF中
MN=CF,NP=CD,
∴Rt△NPM≌Rt△CDF(HL)
∴PM=DF
设PM=DF=x,则CM=PC+PM=![]() +x,
+x,
∵由(1)得MN⊥CF,G为CF中点
∴MN垂直平分CF
∴MF=MC
∴∠MFC=∠FCD=15°
∴∠DMF=∠MFC+∠FCD=30°
∴Rt△DMF中,MF=2DF=2x,DM=![]() ,
,
由于MF=MC,即2x=![]() +x
+x
∴x=![]()
∴DF=![]() ,DM=
,DM=![]() ,CM=MF=2
,CM=MF=2![]() ,CD=CM+DM=2
,CD=CM+DM=2![]() +
+![]()
∵∠GCM=∠MCF,∠CGM=∠CDF=90°
∴△CGM∽△CDF
∴![]() ,
,
∴2CG2=CDCM=(2![]() +
+![]() )2
)2![]() =8+4
=8+4![]() ,
,
∴CG2=4+2![]() =12+2
=12+2![]() +(
+(![]() )2=(1+
)2=(1+![]() )2,
)2,
∴FG=CG=1+![]() .
.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案【题目】将从1开始的连续自然数按图规律排列:
列 行 | 第1列 | 第2列 | 第3列 | 第4列 |
第1行 | 1 | 2 | 3 | 4 |
第2行 | 8 | 7 | 6 | 5 |
第3行 | 9 | 10 | 11 | 12 |
第4行 | 16 | 15 | 14 | 13 |
… | … | … | … | … |
第 | … | … | … | … |
规定位于第![]() 行,第
行,第![]() 列的自然数10记为
列的自然数10记为![]() ,自然数15记为
,自然数15记为![]() …按此规律,自然数2018记为______.
…按此规律,自然数2018记为______.