题目内容
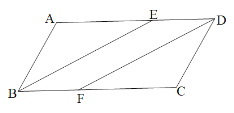
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,以点A为顶点的一个60°的角∠EAF绕点A旋转,∠EAF的两边分别交BC,CD于点E,F,且E,F不与B,C,D重合,连接EF.
(1)求证:BE=CF.
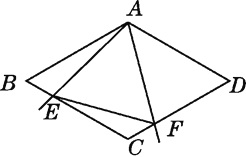
(2)在∠EAF绕点A旋转的过程中,四边形 AECF的面积是否发生变化?如果不变,求出其定值;如果变化,请说明理由.
【答案】(1)证明见解析(2) S四边形AECF=4![]()
【解析】试题分析:(1)连接AC,根据∠BAD=120°和菱形的性质可得∠ABE=∠ACF=60°,然后由∠1+∠2=60°,∠3+∠2=∠EAF=60°得∠1=∠3,再证得△ABC为等边三角形,得AC=AB,进而证得△ABE≌△ACF,由全等三角形的对应边相等即可得出结论;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC可知四边形AECF的面积不变,做出BC边上的高,根据等边三角形的性质和勾股定理求出高,利用三角形的面积公式求出△ABC的面积即为AECF的面积.
试题解析:
(1)证明:如图,连接AC.
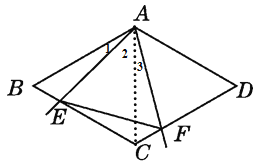
∵四边形ABCD为菱形,
∠BAD=120°,
∴∠ABE=∠ACF=60°,
∠1+∠2=60°,
∵∠3+∠2=∠EAF=60°,
∴∠1=∠3.
∵∠ABC=60°,AB=BC,
∴△ABC为等边三角形,
∴AC=AB,
∴△ABE≌△ACF.
∴BE=CF.
(2)解:四边形AECF的面积不变.
由(1)知△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC.
如图,过A作AM⊥BC于点M,则BM=MC=2,
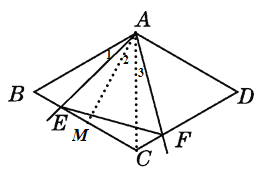
∴AM=![]() =
=![]() =
=![]() .
.
∴S△ABC=![]() BC·AM=
BC·AM=![]() ×4×
×4×![]() =
=![]() .
.
故S四边形AECF=![]() .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案