题目内容
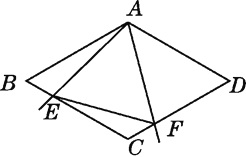
【题目】如图,AB∥CD, AC∥BD, CE平分∠ACD,交BD于点E,点F在CD的延长线上,且∠BEF=∠CEF,若∠DEF=∠EDF,则∠A的度数为_____![]() .
.
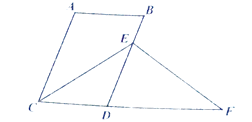
【答案】108
【解析】根据平行线的性质,得到∠A+∠B=180°,∠B=∠BDF,∠A+∠ACD=180°,然后根据角平分线的性质,得到∠ACE=∠ECD=∠CED,然后根据题意和三角形的外角的性质,四边形的内角和求解.
∵CE平分∠ACD
∴∠ACE=∠DCE
∵AB∥CD,AC∥BD,
∴∠A+∠B=180°,∠B=∠BDF,∠ACD+∠A=180°,∠ACE=∠CED
∵∠EDF=∠DEF =∠ECD+∠CED
∴∠CEF=∠FEB=∠CED+∠DEF
设∠B=x,则∠A=180°-x,∠ACE=∠ECD=∠CED=![]() x,
x,
∴∠EDF=x,∠BEF=![]() x
x
∴∠CEB=360°-2×∠BEF=360°-3x
∴∠A+∠B+∠BEC+∠ACE=180°-x+x+360°-3x+![]() x=360°
x=360°
解得x=72°
∴∠A=180°-72°=108°.
故答案为:108.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目