题目内容
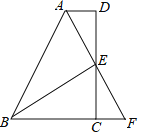
【题目】如图,已知A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC.且已知AB=CD.
(1)试问DB平分EF能成立吗?请说明理由.
(2)若△DEC的边EC沿AC方向移动,其余条件不变,如图,上述结论是否仍成立?请说明理由.
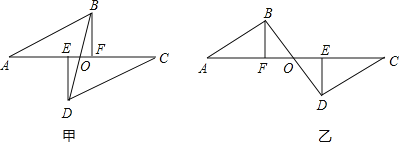
【答案】(1)成立;理由见解析;(2)结论依然成立;理由见解析.
【解析】
(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFO≌△DEO,从而得出OE=0F.DB平分EF
(2)结论仍然成立,同理可以证明得到.
解:(1)OE=0F;
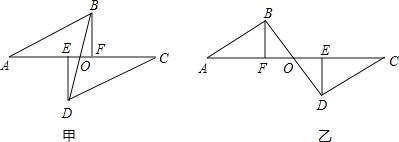
证明:∵DE⊥AC,BF⊥AC,
∴∠DEF=∠BFE=90°.
∵AE=CF,AE+EF=CF+EF.即AF=CE.
在Rt△ABF和Rt△CDE中,
∵![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE.
在△BFO和△DEO中,
∵
∴△BFO≌△DOE(ASA),
∴OE=0F;
(2)结论依然成立.
理由:由AE=CF,得AF=CE,
结合已知得Rt△ABF≌Rt△CDE,
由BF=DE,从而△BFO≌△DEO,
∴FO=EO,
即结论依然成立;

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】为传承经典,某市开展“中华古诗词”朗读大赛,某中学甲、乙两名选手经过八轮预赛后脱颖而出,甲、乙两名学生的成绩如图所示,甲、乙两名学生成绩的相关统计数据如表所示,请结合图表回答下列问题:

平均数 | 方差 | |
甲 |
| 118.25 |
乙 | 80 |
|
(1)甲、乙两名同学预赛成绩的中位数分别是:甲__________分,乙___________分;
(2)王老师说,两个人的平均水平相当,不知道选谁参加决赛,但李老师说,乙同学的成绩稳定,请你先计算出![]() 的值并选择所学过的平均数、方差等统计知识,对两位老师的观点进行解释;
的值并选择所学过的平均数、方差等统计知识,对两位老师的观点进行解释;
(3)若学校想从两名选手中选择一名冲击决赛金牌,会选择谁参加?请说明理由.