题目内容
【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.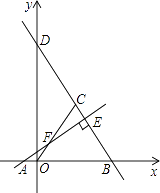
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.
【答案】
(1)
解:∵△OBC是等边三角形,
∴∠OBC=60°,OC=BC=OB,
∵点B的坐标为(6,0),
∴OB=6,
在Rt△OBD中,∠OBC=60°,OB=6,
∴∠ODB=30°,
∴BD=12,
∴OD= ![]() =6
=6 ![]() ,
,
∴点D的坐标为(0,6 ![]() ),
),
设直线BD的解析式为y=kx+b,则可得 ![]() ,
,
解得: ![]() ,
,
∴直线BD的函数解析式为y=﹣ ![]() x+6
x+6 ![]()
(2)
解:∵∠OCB=60°,∠CEF=90°,
∴∠CFE=30°,
∴∠AFO=30°(对顶角相等),
又∵∠OBC=60°,∠AEB=90°,
∴∠BAE=30°,
∴∠BAE=∠AFO,
∴OF=OA=2
(3)
解:连接BF,OE,如图所示:
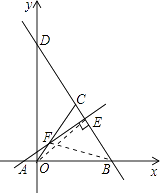
∵A(﹣2,0),B(6,0),
∴AB=8,
在Rt△ABE中,∠ABE=60°,AB=8,
∴BE= ![]() AB=4,
AB=4,
∴CE=BC﹣BE=2,
∴OF=CE=2,
在△COE和△OBF中, 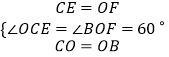 ,
,
∴△COE≌△OBF(SAS),
∴OE=BF.
【解析】(1)根据△OBC是等边三角形,可得∠OBC=60°,在Rt△PBD中,解得OD的长度,得出点D的坐标,利用待定系数法求出直线BD的解析式即可;(2)分别求出∠BAE和∠AFO的度数,即可得出OF=OA=2.(3)在Rt△ABE中,先求出BE,继而得出CE=OF,证明△COE≌△OBF,可得BF和OE的数量关系.
【考点精析】利用一次函数的图象和性质对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

 阅读快车系列答案
阅读快车系列答案