��Ŀ����
����Ŀ�������dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������Ľ�ϣ��о��������Ƿ�����������Ҫ�Ĺ��ɣ�������A�㡢B���ʾ����Ϊa��b����A��B����֮��ľ���AB=|a��b|����a��b����ɼ�ΪAB=a��b��
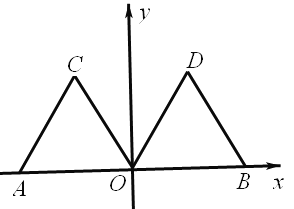
��ͼ��
��֪��������A��B���㣬�ֱ��ʾ����Ϊ��10��8����A��ÿ��3����λ���ٶ����������������˶�����B��ÿ��2����λ���������˶������˶�ʱ��Ϊt�루t��0����
���ۺ����ã���
��1����A�˶�2�������λ�õĵ��ʾ����Ϊ�� ������B�˶�3�������λ�õĵ��ʾ����Ϊ�� ����
��2�����ǰ�������ʽ�˶���A��B���㾭�������������������������ʾ������ʲô��
��3�����ǰ�������ʽ�˶���A��B���㾭������������2����λ���ȣ�
![]()
���𰸡�(1) ��4��2��(2) A��B���㾭��3.6��������������������ʾ������0.8��(3) ����3.2s��4s��A��B�������2����λ��
��������
��1����A�˶�t�������λ�õĵ��ʾ����=�˶���ʼǰA���ʾ����+��A�˶���·�̣���B�˶�t�������λ�õĵ��ʾ����=�˶���ʼǰB���ʾ����-��B�˶���·�̣�
��2�������ǰ�������ʽ�˶���A��B���㾭��t���������������ϵΪ����A�˶���·��+��B�˶���·��=18�������г����̣��ⷽ�̼��ɣ�
��3���������ۢ���A������ߣ�B�����ұߣ���8��2t������10+3t��=2������A�����ұߣ�B������ߣ���10��3t����8��2t��=2����⼴�ɵó�����.
��1����10+3��2=��4��8��2��3=2��
�ʴ�Ϊ����4��2��
��2������������10+3t=8��2t��
��ã� t=3.6��
����10+3t=0.8��
��A��B���㾭��3.6��������������������ʾ������0.8��
��3���������ۣ�
����A������ߣ�B�����ұߣ���8��2t������10+3t��=2��
��ã�t=3.2��
����A�����ұߣ�B������ߣ���10��3t����8��2t��=2��
��ã�t=4��
�𣺾���3.2s��4s��A��B�������2����λ��

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�