题目内容
求证:两条直线被第三条直线所截,如果同旁内角的角平分线互相垂直, 那么这两条直线互相平行.
证明过程见试题解析.
解析试题分析:两条直线被第三条直线所截,同旁内角的角平分线互相垂直,根据角平分线的性质求出这对同旁内角和的一半是90°,得到一对同旁内角的和是180°,所以两条直线平行.
试题解析:如图,已知AB、CD被EF所截,EG、FG分别平分∠BEF、∠DFE,且EG⊥FG,求证:AB∥CD.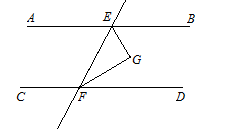
证明:∵EG⊥FG,∴∠GEF+∠EFG=90°,∵EG、FG分别平分∠BEF、∠DFE,∴∠BEF+∠DFE=2(∠GEF+∠EFG)=180°,∴AB∥CD.
考点:1.平行线的判定;2.角平分线的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
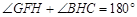 ,
, .
.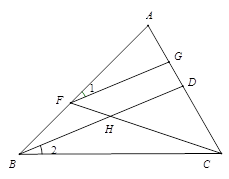
 是直角,
是直角, ,
, 是
是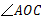 的平分线,
的平分线, 是
是 的平分线.
的平分线.
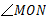 的大小.
的大小.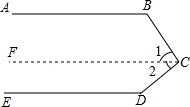


 ,则
,则 的值为
的值为