题目内容
已知:如图, 是直角,
是直角, ,
, 是
是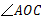 的平分线,
的平分线, 是
是 的平分线.
的平分线.
(1)求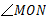 的大小.
的大小.
(2)当锐角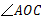 的大小发生改变时,
的大小发生改变时,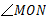 的大小是否发生改变?为什么?
的大小是否发生改变?为什么?
(1)45° (2)∠MON的大小不发生改变,理由见解析
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知:如图, 是直角,
是直角, ,
, 是
是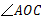 的平分线,
的平分线, 是
是 的平分线.
的平分线.
(1)求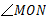 的大小.
的大小.
(2)当锐角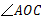 的大小发生改变时,
的大小发生改变时,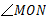 的大小是否发生改变?为什么?
的大小是否发生改变?为什么?
(1)45° (2)∠MON的大小不发生改变,理由见解析
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案