题目内容
已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
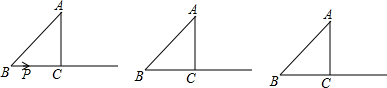
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值

分析:(1)直接根据勾股定理求出BC的长度;
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(3)当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(3)当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
解答:解:(1)在Rt△ABC中,BC2=AB2-AC2=52-32=16,
∴BC=4(cm);
(2)由题意知BP=tcm,
①当∠APB为直角时,点P与点C重合,BP=BC=4cm,即t=4;
②当∠BAP为直角时,BP=tcm,CP=(t-4)cm,AC=3cm,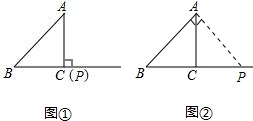
在Rt△ACP中,
AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
即:52+[32+(t-4)2]=t2,
解得:t=
,
故当△ABP为直角三角形时,t=4或t=
;
(3)①当AB=BP时,t=5;
②当AB=AP时,BP=2BC=8cm,t=8;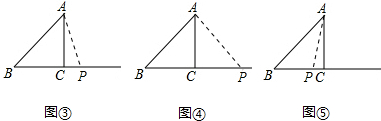
③当BP=AP时,AP=BP=tcm,CP=|t-4|cm,AC=3cm,
在Rt△ACP中,AP2=AC2+CP2,
所以t2=32+(t-4)2,
解得:t=
,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=
.
∴BC=4(cm);
(2)由题意知BP=tcm,
①当∠APB为直角时,点P与点C重合,BP=BC=4cm,即t=4;
②当∠BAP为直角时,BP=tcm,CP=(t-4)cm,AC=3cm,

在Rt△ACP中,
AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
即:52+[32+(t-4)2]=t2,
解得:t=
| 25 |
| 4 |
故当△ABP为直角三角形时,t=4或t=
| 25 |
| 4 |
(3)①当AB=BP时,t=5;
②当AB=AP时,BP=2BC=8cm,t=8;

③当BP=AP时,AP=BP=tcm,CP=|t-4|cm,AC=3cm,
在Rt△ACP中,AP2=AC2+CP2,
所以t2=32+(t-4)2,
解得:t=
| 25 |
| 8 |
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=
| 25 |
| 8 |
点评:本题考查了勾股定理以及等腰三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
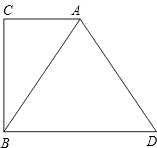 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.