题目内容
 (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.分析:①连接OE,由OD与AB平行得到一对同位角相等,一对内错角相等,再由半径相等,利用等边对等角得到一对角相等,等量代换得到一对角相等,利用SAS得出三角形OCD与三角形OED全等,由全等三角形对应角相等及垂直的定义得到ED垂直于OE,即ED为圆O的切线;
②由第一问的全等得到CD=ED,再由BC为圆的切线,BA为圆的割线,利用切割线定理列出关系式,根据O为AC中点,OD平行于AB,得到D为BC中点,即OD为三角形ABC的中位线,利用三角形中位线定理得到AB=2OD,BC=2CD=2DE,代换即可得证.
②由第一问的全等得到CD=ED,再由BC为圆的切线,BA为圆的割线,利用切割线定理列出关系式,根据O为AC中点,OD平行于AB,得到D为BC中点,即OD为三角形ABC的中位线,利用三角形中位线定理得到AB=2OD,BC=2CD=2DE,代换即可得证.
解答: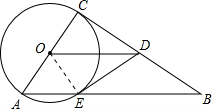 证明:①连接OE,
证明:①连接OE,
∵OD∥AB,
∴∠COD=∠A,∠DOE=∠OEA,
∵OA=OE,
∴∠A=∠OEA,
∴∠COD=∠DOE,
在△COD和△EOD中,
,
∴△COD≌△EOD(SAS),
∴∠OCD=∠OED=90°,
∴DE⊥OE,
则DE为圆O的切线;
②由△COD≌△EOD,得到CD=ED,
∵BC为圆O的切线,BA为圆O的割线,
∴BC2=BE•BA,
∵O为AC的中点,OD∥AB,
∴D为BC的中点,即OD为△ABC的中位线,
∴BA=2OD,BC=2CD=2DE,
则4DE2=BE•2OD,即2DE2=BE•OD.
 证明:①连接OE,
证明:①连接OE,∵OD∥AB,
∴∠COD=∠A,∠DOE=∠OEA,
∵OA=OE,
∴∠A=∠OEA,
∴∠COD=∠DOE,
在△COD和△EOD中,
|
∴△COD≌△EOD(SAS),
∴∠OCD=∠OED=90°,
∴DE⊥OE,
则DE为圆O的切线;
②由△COD≌△EOD,得到CD=ED,
∵BC为圆O的切线,BA为圆O的割线,
∴BC2=BE•BA,
∵O为AC的中点,OD∥AB,
∴D为BC的中点,即OD为△ABC的中位线,
∴BA=2OD,BC=2CD=2DE,
则4DE2=BE•2OD,即2DE2=BE•OD.
点评:此题考查了切线的判定,切割线定理,全等三角形的判定与性质,中位线定理,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
 (1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=
(1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=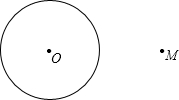 (1997•陕西)已知:⊙O及⊙O外一点M,求作:⊙O的外切△MAB且使MA=MB.
(1997•陕西)已知:⊙O及⊙O外一点M,求作:⊙O的外切△MAB且使MA=MB.