题目内容
（2013•闵行区三模）已知：如图，△ABC是等边三角形，点D在边BC上，且△ADE是等边三角形．过点E作EF∥BC，EF分别与线段AB、AC、AD相交于点F、G、H，联结CE．（1）求证：四边形BCEF是平行四边形；
（2）如果AD⊥BC，求证：BC=2FG．
分析：（1）通过全等三角形△BAD≌△CAE（SAS）的对应角相等判定∠B=∠ACE=60°．则∠ACE=∠BAC．所以根据平行线的判定知BF∥CE．又EF∥BC，故两组对边互相平行的四边形是平行四边形，即四边形BCEF是平行四边形；
（2）由垂直得到直角，即由AD⊥BC，得到∠ADC=90°．然后根据（1）中的平行线得到∠AHE=∠ADC=90°．即EH⊥AD．又△ADE是等边三角形，所以EA=ED．AH=DH．再根据平行线分线段成比例得到
=
=1．即AF=BF，同理可得AG=CG．故BC=2FG．
（2）由垂直得到直角，即由AD⊥BC，得到∠ADC=90°．然后根据（1）中的平行线得到∠AHE=∠ADC=90°．即EH⊥AD．又△ADE是等边三角形，所以EA=ED．AH=DH．再根据平行线分线段成比例得到
| AF |
| FB |
| AH |
| DH |
解答：证明：（1）∵△ABC是等边三角形，
∴AB=AC，∠BAC=∠B=60°．
同理可知，AD=AE，∠DAE=60°．
即得∠BAC=∠DAE．
∴∠BAC-∠DAC=∠DAE-∠DAC．
即得∠BAD=∠CAE．
∴在△BAD和△CAE中，
∴△BAD≌△CAE（SAS）．
∴∠B=∠ACE=60°．
∴∠ACE=∠BAC．
∴BF∥CE．
又∵EF∥BC，
∴四边形BCEF是平行四边形；
（2）∵AD⊥BC，
∴∠ADC=90°．
又∵EF∥BC，
∴∠AHE=∠ADC=90°．即EH⊥AD．
又∵△ADE是等边三角形，
∴EA=ED．
∴AH=DH．
∵EF∥BC，∴
=
=1．
∴AF=BF，
同理可得 AG=CG．
∴BC=2FG．
∴AB=AC，∠BAC=∠B=60°．
同理可知，AD=AE，∠DAE=60°．
即得∠BAC=∠DAE．
∴∠BAC-∠DAC=∠DAE-∠DAC．
即得∠BAD=∠CAE．
∴在△BAD和△CAE中，
|
∴△BAD≌△CAE（SAS）．
∴∠B=∠ACE=60°．
∴∠ACE=∠BAC．
∴BF∥CE．
又∵EF∥BC，
∴四边形BCEF是平行四边形；
（2）∵AD⊥BC，
∴∠ADC=90°．
又∵EF∥BC，
∴∠AHE=∠ADC=90°．即EH⊥AD．
又∵△ADE是等边三角形，
∴EA=ED．
∴AH=DH．
∵EF∥BC，∴
| AF |
| FB |
| AH |
| DH |
∴AF=BF，
同理可得 AG=CG．
∴BC=2FG．
点评：本题综合考查了平行四边形的判定与性质，全等三角形的判定与性质以及平行线分线段成比例等知识点，综合性比较强，需要同学们对知识有一个系统的掌握．
练习册系列答案
名校课堂系列答案
相关题目
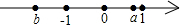（2013•闵行区三模）已知实数a、b在数轴上的位置如图所示，那么下列等式成立的是（ ）