题目内容
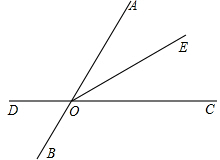 如图,直线AB,CD相交于点O,OE是∠AOC的角平分线,∠DOE=5∠AOE,求∠BOD的度数.
如图,直线AB,CD相交于点O,OE是∠AOC的角平分线,∠DOE=5∠AOE,求∠BOD的度数.分析:根据角平分线定义得出∠AOE=∠COE,得出∠DOE=5∠COE,根据∠DOE+∠COE=180°,求出∠COE=∠AOE=30°,求出∠AOC的度数,根据对顶角相等求出即可.
解答:解:∵OE是∠AOC的角平分线,
∴∠AOE=∠COE,
∵∠DOE=5∠AOE,
∴∠DOE=5∠COE,
∵∠DOE+∠COE=180°,
∴∠COE=
×180°=30°,
∴∠AOC=∠AOE+∠COE=60°,
∴∠BOD=∠AOC=60°.
∴∠AOE=∠COE,
∵∠DOE=5∠AOE,
∴∠DOE=5∠COE,
∵∠DOE+∠COE=180°,
∴∠COE=
| 1 |
| 6 |
∴∠AOC=∠AOE+∠COE=60°,
∴∠BOD=∠AOC=60°.
点评:本题考查了邻补角定义,对顶角相等,角平分线定义的应用,关键是求出∠COE的度数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.
21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.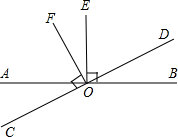 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.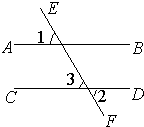 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD, 如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数=
如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数=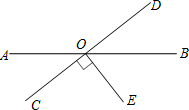 如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.
如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.