题目内容
计算及解方程
(1) +
+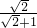 -
-
(2)(2 -3
-3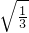 )×6
)×6
(3)3a -
- (a≥0)
(a≥0)
(4)(2 +3)(2
+3)(2 -3)+(2
-3)+(2 +3)2
+3)2
(5)9(x-2)2-121=0
(6)3y(y-1)=2(y-1)
(7)x2-8x+1=0 (用配方法)
(8)2x2-3x=-5x-5.
解:(1)原式=3 +
+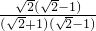 -
-
 ,
,
=3 +2-
+2- -
- ,
,
=2+ ;
;
(2)原式=2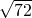 -3
-3 =12
=12 -3
-3 =10
=10 ;
;
(3)原式=3a -2
-2 =(3a-2)
=(3a-2) ;
;
(4)原式=8-9+8+9+12 =16+12
=16+12 ;
;
(5)移项得:9(x-2)2=121,
两边同时除以9得:(x-2)2= ,
,
开方得:x-2=± ,
,
则:x-2= ,x-2=-
,x-2=- ,
,
解得:x1= ,x2=-
,x2=- ;
;
(6)移项得:3y(y-1)-2(y-1)=0,
(3y-2)(y-1)=0,
则:3y-2=0,y-1=0,
解得:y1= ,y2=1;
,y2=1;
(7)移项得:x2-8x=0-1,
配方得:x2-8x+16=-1+16,
(x-4)2=15,
开方得:x-4=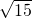 ,
,
则x-4= ,x-4=-
,x-4=- ,
,
解得:x1= +4,x2=-
+4,x2=- +4;
+4;
(8)移项得:2x2-3x+5x+5=0,
整理得:2x2+2x+5=0,
∵a=2,b=2,c=-5,
∴x=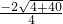 =
=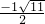 ,
,
∴x1= .x2=
.x2=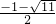 .
.
分析:(1)首先把二次根式进行化简,再合并同类二次根式即可;
(2)利用乘法分配律,用括号里的每一项都乘以6,再化简二次根式,合并同类二次根式即可;
(3)首先把二次根式进行化简,再合并同类二次根式即可;
(4)先利用平方差公式与完全平方公式进行计算,再计算有理数的加减法即可;
(5)首先把方程化为(x-2)2= ,再两边同时开方即可得到一元一次方程,再解一元一次方程即可;
,再两边同时开方即可得到一元一次方程,再解一元一次方程即可;
(6)首先移项,再利用因式分解法可得(3y-2)(y-1)=0,进而可得一元一次方程,再解一元一次方程即可;
(7)首先把方程化为x2-8x=0-1,再把方程的左边分解因式即可;
(8)先把方程整理可得:2x2+2x+5=0,再利用公式法解方程即可.
点评:此题主要考查了二次根式的混合运算,一元二次方程的解法,关键是熟练掌握二次根式的化简,以及一元二次方程的解法.
 +
+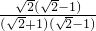 -
-
 ,
,=3
 +2-
+2- -
- ,
,=2+
 ;
;(2)原式=2
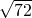 -3
-3 =12
=12 -3
-3 =10
=10 ;
;(3)原式=3a
 -2
-2 =(3a-2)
=(3a-2) ;
;(4)原式=8-9+8+9+12
 =16+12
=16+12 ;
;(5)移项得:9(x-2)2=121,
两边同时除以9得:(x-2)2=
 ,
,开方得:x-2=±
 ,
,则:x-2=
 ,x-2=-
,x-2=- ,
,解得:x1=
 ,x2=-
,x2=- ;
;(6)移项得:3y(y-1)-2(y-1)=0,
(3y-2)(y-1)=0,
则:3y-2=0,y-1=0,
解得:y1=
 ,y2=1;
,y2=1;(7)移项得:x2-8x=0-1,
配方得:x2-8x+16=-1+16,
(x-4)2=15,
开方得:x-4=
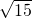 ,
,则x-4=
 ,x-4=-
,x-4=- ,
,解得:x1=
 +4,x2=-
+4,x2=- +4;
+4;(8)移项得:2x2-3x+5x+5=0,
整理得:2x2+2x+5=0,
∵a=2,b=2,c=-5,
∴x=
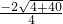 =
=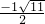 ,
,∴x1=
 .x2=
.x2=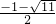 .
.分析:(1)首先把二次根式进行化简,再合并同类二次根式即可;
(2)利用乘法分配律,用括号里的每一项都乘以6,再化简二次根式,合并同类二次根式即可;
(3)首先把二次根式进行化简,再合并同类二次根式即可;
(4)先利用平方差公式与完全平方公式进行计算,再计算有理数的加减法即可;
(5)首先把方程化为(x-2)2=
 ,再两边同时开方即可得到一元一次方程,再解一元一次方程即可;
,再两边同时开方即可得到一元一次方程,再解一元一次方程即可;(6)首先移项,再利用因式分解法可得(3y-2)(y-1)=0,进而可得一元一次方程,再解一元一次方程即可;
(7)首先把方程化为x2-8x=0-1,再把方程的左边分解因式即可;
(8)先把方程整理可得:2x2+2x+5=0,再利用公式法解方程即可.
点评:此题主要考查了二次根式的混合运算,一元二次方程的解法,关键是熟练掌握二次根式的化简,以及一元二次方程的解法.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目