题目内容
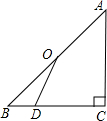 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.操作:在图中作OE⊥OD交AC于E,连接DE.
问题:(1)观察并猜测,无论∠DOE绕着点O旋转到任何位置,OD和OE始终有何数量关系?(直接写出答案)
(2)如图所示,若BD=2,AE=4,求△DOE的面积.
(说明:如果经过思考分析,没有找到解决(2)中的问题的方法,请直接验证(1)中猜测的结论)
分析:(1)可连接OC,求△COE≌△BOD则△DOE为等腰三角形,可得OD=OE,
(2)第二问中求出△DOE的高OF及一底边长DE即可,代入面积公式求解面积.
(2)第二问中求出△DOE的高OF及一底边长DE即可,代入面积公式求解面积.
解答: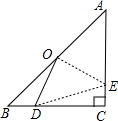 解:(1)作图
解:(1)作图
连接OC,如下图
∵OC=OB,∠ACO=∠B=45°,∠BOD=∠COE
则△COE≌△BOD
∴OD=OE;
(2)连接OC,先证△OBD≌△OEC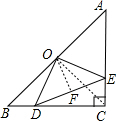
∵BD=2,AE=4,
∴得到CE=BD=2,
∴CD=AE=4,∴在Rt△CDE中,DE=2
作OF⊥DE,
在Rt△DOE中,∴OF2=DF•EF,
∴OF=
S=
•DE•OF=
•2
•
=5
∴△ODE的面积为5.
 解:(1)作图
解:(1)作图连接OC,如下图
∵OC=OB,∠ACO=∠B=45°,∠BOD=∠COE
则△COE≌△BOD
∴OD=OE;
(2)连接OC,先证△OBD≌△OEC

∵BD=2,AE=4,
∴得到CE=BD=2,
∴CD=AE=4,∴在Rt△CDE中,DE=2
| 5 |
作OF⊥DE,
在Rt△DOE中,∴OF2=DF•EF,
∴OF=
| 5 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∴△ODE的面积为5.
点评:本题考查了等腰三角形的性质及全等三角形的性质及判定;正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
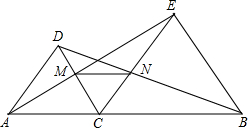 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 已知:如图,点P是等边三角形ABC内一点,
已知:如图,点P是等边三角形ABC内一点, 23、已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.
23、已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数. 已知:如图,点P是等边三角形ABC内一点,
已知:如图,点P是等边三角形ABC内一点,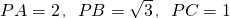 ,求∠BPC的度数.
,求∠BPC的度数. 已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.
已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.