题目内容
 已知:如图,点P是等边三角形ABC内一点,PA=2,PB=
已知:如图,点P是等边三角形ABC内一点,PA=2,PB=| 3 |
分析:以BP边作等边三角形BPD,连接AD,根据等边三角形的每一个角都等于60°推出∠ABD=∠CBP,然后利用边角边证明△ABD与△CBP全等,根据全等三角形对应边相等可得AD=CP=1,对应角相等可得∠BPC=∠BDA,再利用勾股定理逆定理证明△ADP是∠ADP=90°的直角三角形,从而求出∠ADB的度数,即∠BPC的度数.
解答: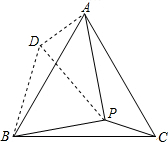 解:以BP为边作等边三角形BPD,连接AD,
解:以BP为边作等边三角形BPD,连接AD,
则BD=BP=DP=
,∠DBP=∠BDP=60°,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵∠ABD+∠ABP=∠CBP+∠ABP=60°,
∴∠ABD=∠CBP,
在△ABD与△CBP中,
,
∴△ABD≌△CBP(SAS),----------------------------(3分)
∴∠BPC=∠BDA,AD=PC=1,
在△ADP中,∵PA=2,PD=
,AD=1,
∴AP2=DP2+AD2,
∴△APD是直角三角形,---------------------------(4分)
∴∠ADP=90°,
∴∠ADB=∠ADP+∠BDP=150°,
∴∠BPC=150°.-----------------------------------(5分)
 解:以BP为边作等边三角形BPD,连接AD,
解:以BP为边作等边三角形BPD,连接AD,则BD=BP=DP=
| 3 |
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵∠ABD+∠ABP=∠CBP+∠ABP=60°,
∴∠ABD=∠CBP,
在△ABD与△CBP中,
|
∴△ABD≌△CBP(SAS),----------------------------(3分)
∴∠BPC=∠BDA,AD=PC=1,
在△ADP中,∵PA=2,PD=
| 3 |
∴AP2=DP2+AD2,
∴△APD是直角三角形,---------------------------(4分)
∴∠ADP=90°,
∴∠ADB=∠ADP+∠BDP=150°,
∴∠BPC=150°.-----------------------------------(5分)
点评:本题考查了等边三角形的性质,全等三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和,勾股定理逆定理,作出辅助线,把PA、PB、PC的长度转化为一个三角形三条边,构造出直角三角形是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
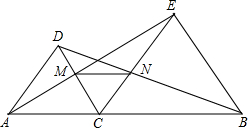 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 23、已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.
23、已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数. 已知:如图,点P是等边三角形ABC内一点,
已知:如图,点P是等边三角形ABC内一点,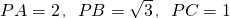 ,求∠BPC的度数.
,求∠BPC的度数. 已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.
已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.