题目内容
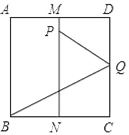
【题目】如图，面积为1的正方形ABCD中，M，N分别为AD、BC的中点，将C点折至MN上，落在P点的位置，折痕为BQ，连接PQ．以PQ为边长的正方形的面积等于______．
【答案】
【解析】
根据折叠的性质，可得PQ=QC，∠PBQ=∠QBC=30°；再在Rt△BCQ中，根据三角函数的定义可求得PQ的值，进而可得答案．
解：由折法知，点P是点C关于折痕BQ的对称点
∴BQ垂直平分PC，BC=BP
∵M，N分别为AD，BC边上的中点，且ABCD是正方形
∴BP=PC
∴BC=BP=PC
∴△PBC是等边三角形
∴∠PBQ=∠QBC==
∠PBC=×60°=30°
由折法知PQ=QC．
在Rt△BCQ中，
，
∴
．
∴以PQ为边的正方形的面积为．
故答案为：．
练习册系列答案
每课必练系列答案
相关题目
【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展，小明计划给朋友快递一部分物品，经了解有甲乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．
（1）根据题意，填写下表：
重量（千克） 费用（元） | 0.5 | 1 | 3 | 4 | … |
甲公司 | _________ | 22 | _________ | 67 | … |
乙公司 | 11 | ________ | 51 | _________ | … |
（2）请分别写出甲乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；
（3）小明应选择哪家快递公司更省钱？
