Question

【题目】如图，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），求该光盘的直径是多少？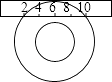

Answer 1

【答案】解：过点O作OA垂直直尺与点A，连接OB，设OB=r，
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”，
∴AB=4，
∵刻度尺宽2cm，
∴OA=r﹣2，
在Rt△OAB中，
OA2+AB2=OB2 ， 即（r﹣2）2+42=r2 ，
解得r=5，
则该光盘的直径是10cm．

【解析】先过点O作OA垂直直尺与点A，连接OB，再设OB=r，利用勾股定理求出r的值即可得出答案．
【考点精析】本题主要考查了勾股定理的概念和垂径定理的推论的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；推论1：A、平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧B、弦的垂直平分线经过圆心，并且平分弦所对的两条弧C、平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；推论2 ：圆的两条平行弦所夹的弧相等才能正确解答此题．