题目内容
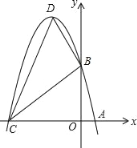
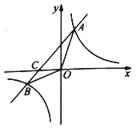
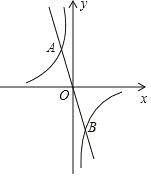
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.
【答案】(1)y=﹣![]() ,B(1,﹣2);(2)x
,B(1,﹣2);(2)x![]() ﹣1 或 x>0;(3)
﹣1 或 x>0;(3)![]() .
.
【解析】
(1)已知点A的坐标代入正比例函数可求出a,再把点A坐标代入可求出反比例函数解析式;又因为正比例函数和反比例函数交点是A、B,可知A、B两点关于原点对称从而可求出B点坐标
(2)观察图像即可得出
(3)根据题意补全图形把三角形的面积转换成梯形的面积然后根据已知求解一元二次方程,把不符合实际情况的根舍掉即可得出答案。
(1)把 A(﹣1,a)代入 y=﹣2x,可得 a=2,
∴A(﹣1,2),
把 A(﹣1,2)代入 y=![]() ,可得 k=﹣2,
,可得 k=﹣2,
∴反比例函数的表达式为 y=﹣![]() ,
,
∵点 B 与点 A 关于原点对称,
∴B(1,﹣2).
(2)∵A(﹣1,2),
∴y≤2 的取值范围是 x![]() ﹣1 或 x>0;
﹣1 或 x>0;
(3)作 BM⊥x 轴于 M,PN⊥x 轴于 N,
∵S 梯形 MBPN=S△POB=1,
设 P(m,﹣![]() ),则
),则![]() ×(2+
×(2+![]() )(m﹣1)=1 或
)(m﹣1)=1 或![]() ×(2+
×(2+![]() )(1﹣m)=1整理得,m2﹣m﹣1=0 或 m2+m+1=0,
)(1﹣m)=1整理得,m2﹣m﹣1=0 或 m2+m+1=0,
解得 m=![]()
∴P 点的横坐标![]()

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目