题目内容
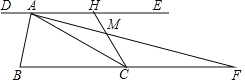
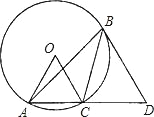
【题目】如图,在⊙O 的内接△ABC 中,∠ABC=30°,AC 的延长线与过点 B 的⊙O 的切线相交于点 D,若⊙O 的半径 OC=1,BD∥OC,则 CD 的长为( )
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作辅助线OB、CE构建正方形CEBO.根据圆周角定理(同弧所对的圆周角是所对的圆心角的一半)求得∠OAC=2∠ABC=60°,然后由切线的性质及平行线的性质求得OB⊥OC,OB⊥BD;再根据圆的半径都相等知OB=OC,所以判定四边形CEBO是正方形,然后在直角三角形CDE中利用正弦三角函数sin∠D=sin60°求CD的长度并作出选择.
连接OB,过点C作CE⊥BD于点E,
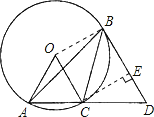
∵∠ABC=30°,
∴∠AOC=60°(同弧所对的圆周角是所对的圆心角的一半);
∵OA=OC(⊙O的半径),
∴∠ACO=∠OAC=60°(等边对等角),
又BD∥OC,
∴∠ACO=∠D=60°(两直线平行,同位角相等),
∴∠OCD=120°(两直线平行,同旁内角互补),
∵BD是⊙O的切线,
∴OB⊥OC,OB⊥BD,
又∵OB=OC,
∴四边形CEBO是正方形,
∴CE=OB=1,
∴CD=![]() =
=![]() ,
,
故选:B.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目