题目内容
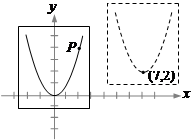
二次函数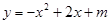 的图象与
的图象与 轴的一个交点为A
轴的一个交点为A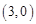 ,另一个交点为B,与
,另一个交点为B,与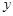 轴交于点C.
轴交于点C.
(1)求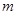 的值及点B、点C的坐标;
的值及点B、点C的坐标;
(2)直接写出当 时,
时, 的取值范围;
的取值范围;
(3)直接写出当 时,
时,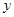 的取值范围.
的取值范围.
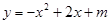 的图象与
的图象与 轴的一个交点为A
轴的一个交点为A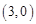 ,另一个交点为B,与
,另一个交点为B,与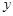 轴交于点C.
轴交于点C.(1)求
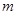 的值及点B、点C的坐标;
的值及点B、点C的坐标;(2)直接写出当
 时,
时, 的取值范围;
的取值范围;(3)直接写出当
 时,
时,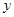 的取值范围.
的取值范围.(1)B(-1,0),C(0,3);(2)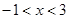 ;(3)0≤y≤4
;(3)0≤y≤4
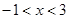 ;(3)0≤y≤4
;(3)0≤y≤4试题分析:(1)由题意把A
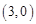 代入二次函数
代入二次函数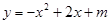 即可求得m的值,从而可以求得结果;
即可求得m的值,从而可以求得结果;(2)根据二次函数的图象的开口方向及与
 轴的交点坐标即可判断;
轴的交点坐标即可判断;(3)分别求出
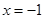 与
与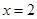 时对应的y值,再结合函数图象的顶点坐标即可得到结果.
时对应的y值,再结合函数图象的顶点坐标即可得到结果.(1)由题意得:0=-9+6+m,解得m=3
∴
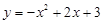
当
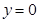 时,
时,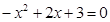 ,解得
,解得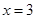 或
或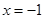 ;当
;当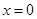 时,
时,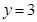
∴抛物线与x轴的另一交点B(-1,0),与y轴交点C(0,3);
(2)当
 时,
时,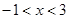 ;
;(3)当-1≤x≤2时,0≤y≤4.
点评:解答本题的关键是熟练掌握x轴上的点的纵坐标为0,y轴上的点的横坐标为0.

练习册系列答案
相关题目
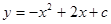 经过点C,交x轴负半轴于点A.
经过点C,交x轴负半轴于点A.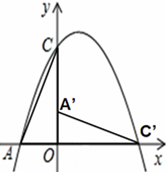
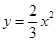 的图像如图所示,点A0位于坐标原点,A1,A2,A3,…,A2012在y轴的正半轴上,B1,B2,B3,…B2012在函数
的图像如图所示,点A0位于坐标原点,A1,A2,A3,…,A2012在y轴的正半轴上,B1,B2,B3,…B2012在函数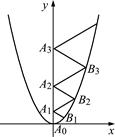

 化成
化成 的形式,则
的形式,则 = .
= .
 ,
,

 ,
,
 的图象上,若△ABC的面积为2,则这样的C点有
的图象上,若△ABC的面积为2,则这样的C点有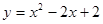 与y轴交点坐标为( )
与y轴交点坐标为( )