题目内容
【题目】如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B. 
(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;
(2)填空: ①当DP=cm时,四边形AOBD是菱形;
②当DP=cm时,四边形AOBP是正方形.
【答案】
(1)解:连接OA,AC
∵PA是⊙O的切线,
∴OA⊥PA,
在Rt△AOP中,∠AOP=90°﹣∠APO=90°﹣30°=60°,
∴∠ACP=30°,
∵∠APO=30°
∴∠ACP=∠APO,
∴AC=AP,
∴△ACP是等腰三角形

(2)1;![]()
【解析】解:(2) ①DP=1,理由如下:
∵四边形AOBD是菱形,
∴OA=AD=OD,
∴∠AOP=60°,
∴OP=2OA,DP=OD.
∴DP=1,
②DP= ![]() ,理由如下:
,理由如下:
∵四边形AOBP是正方形,
∴∠AOP=45°,
∵OA=PA=1,OP= ![]() ,
,
∴DP=OP﹣1
∴DP= ![]() .
.
(1)利用切线的性质可得OC⊥PC.利用同弧所对的圆周角等于圆心角的一半,求得∠ACP=30°,从而求得.(2)①要使四边形AOBD是菱形,则OA=AD=OD,所以∠AOP=60°,所以OP=2OA,DP=OD.②要使四边形AOBP是正方形,则必须∠AOP=45°,OA=PA=1,则OP= ![]() ,所以DP=OP﹣1.
,所以DP=OP﹣1.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | n |
B.文学类 | 14 | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
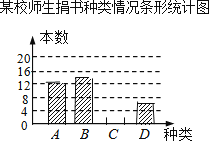
(1)统计表中的m= , n=;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?