题目内容
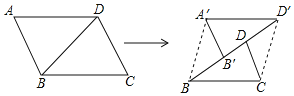
【题目】在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.
(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为____________;
(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.
求证:四边形BGHD是平行四边形;
(3)如图3,对角线 AC、BD相交于点M, AE与BD交于点P, AF与BD交于点N. 直接写出BP、PM、MN、ND的数量关系.

【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]() .
.
【解析】
(1)连接AC,根据三角形中线把三角形分成两个面积相等的三角形进行解答即可得;
(2)连接EF,根据三角形中位线定理可得到BD与GH平行且相等,由此即可得证;
(3)如图,延长PE至点Q,使EQ=EP,连接CQ,延长NF至点O,使OF=NG,连接CO,通过证明△BPE≌△CQE可得BP=CQ,BP//CQ,同理:CO=ND,CO//ND,从而可得Q、C、O三点共线,继而通过证明△APM∽△AQC,可得PM:CQ=AM:AC,同理:MN:CO=AM:AC,即可得答案.
(1)如图,连接AC,则有S△ABC+S△ACD= S四边形ABCD=5,
∵E、F分别为BC、CD中点,
∴S△AEC=![]() S△ABC,S△AFC=
S△ABC,S△AFC=![]() S△ADC,
S△ADC,
∴S四边形AECF=S△AEC+S△AFC=![]() S△ABC+
S△ABC+![]() S△ADC=
S△ADC=![]() S四边形ABCD=
S四边形ABCD=![]() ,
,
故答案为:![]() ;
;

(2)如图,连接EF,
∵E、F分别是BC,CD的中点,
∴EF∥BD,EF=![]() BD.,
BD.,
∵EG=AE,FH=AF,
∴EF∥GH,EF=![]() GH.,
GH.,
∴BD∥GH,BD=GH.,
∴四边形BGHD是平行四边形;

(3)如图,延长PE至点Q,使EQ=EP,连接CQ,
延长NF至点O,使OF=NG,连接CO,
在△BPE和△CQE中
 ,
,
∴△BPE≌△CQE(SAS),
∴BP=CQ,∠PBE=∠QCE,
∴BP//CQ,
同理:CO=ND,CO//ND,
∴Q、C、O三点共线,
∴BD//OQ,
∴△APM∽△AQC,
∴PM:CQ=AM:AC,
同理:MN:CO=AM:AC,
∴![]() .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】定向越野作为一种新兴的运动项目,深受人们的喜爱. 这种定向运动是利用地图和指北针到访地图上所指示的各个点标,以最短时间按序到达所有点标者为胜. 下面是我区某校进行定向越野活动中,中年男子组的成绩(单位:分:秒).
9:01 14:45 9:46 19:22 11:20 18:47 11:40 12:32 11:52 13:45
22:27 15:00 17:30 13:22 18:34 10:45 19:24 16:26 21:33 15:31
19:50 14:27 15:55 16:07 20:43 12:13 21:41 14:57 11:39 12:45
12:57 15:31 13:20 14:50 14:57 9:41 12:13 14:27 12:25 12:38
例如,用时最少的赵老师的成绩为9:01,表示赵老师的成绩为9分1秒.

以下是根据某校进行定向越野活动中,中年男子组的成绩中的数据,绘制的统计图表的一部分.
某校中年男子定向越野成绩分段统计表
分组/分 | 频数 | 频率 |
9≤x<11 | 4 | 0.1 |
11≤x<13 | b | 0.275 |
13≤x<15 | 9 | 0.225 |
15≤x<17 | 6 | d |
17≤x<19 | 3 | 0.075 |
19≤x<21 | 4 | 0.1 |
21≤x<23 | 3 | 0.075 |
合计 | a | c |
(1)这组数据的极差是____________;
(2)上表中的a =____________ ,b =____________ , c =____________, d =____________;
(3)补全频数分布直方图.