题目内容
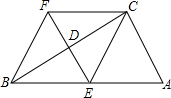（2013•梅州）如图，在四边形ABFC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB与点E，且CF=AE，（1）求证：四边形BECF是菱形；
（2）若四边形BECF为正方形，求∠A的度数．
分析：（1）根据中垂线的性质：中垂线上的点到线段两个端点的距离相等，有BE=EC，BF=FC，根据四边相等的四边形是菱形即可判断；
（2）正方形的性质知，对角线平分一组对角，即∠ABC=45°，进而求出∠A=45度．
（2）正方形的性质知，对角线平分一组对角，即∠ABC=45°，进而求出∠A=45度．
解答：（1）证明：∵EF垂直平分BC，
∴CF=BF，BE=CE，∠BDE=90°，BD=CD，
又∵∠ACB=90°，
∴EF∥AC，
∴BE：AB=DB：BC，
∵D为BC中点，
∴DB：BC=1：2，
∴BE：AB=1：2，
∴E为AB中点，
即BE=AE，
∵CF=AE，
∴CF=BE，
∴CF=FB=BE=CE，
∴四边形BECF是菱形．
（2）解：∵四边形BECF是正方形，
∴∠CBA=45°，
∵∠ACB=90°，
∴∠A=45°．
∴CF=BF，BE=CE，∠BDE=90°，BD=CD，
又∵∠ACB=90°，
∴EF∥AC，
∴BE：AB=DB：BC，
∵D为BC中点，
∴DB：BC=1：2，
∴BE：AB=1：2，
∴E为AB中点，
即BE=AE，
∵CF=AE，
∴CF=BE，
∴CF=FB=BE=CE，
∴四边形BECF是菱形．
（2）解：∵四边形BECF是正方形，
∴∠CBA=45°，
∵∠ACB=90°，
∴∠A=45°．
点评：此题主要考查了菱形的判定方法以及正方形的判定和中垂线的性质、直角三角形的性质等知识，根据已知得出∠CBA=45°是解题关键．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
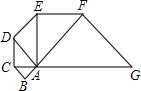（2013•梅州）如图，已知△ABC是腰长为1的等腰直角三形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第2013个等腰直角三角形的斜边长是
（2013•梅州）如图，在平面直角坐标系中，A（-2，2），B（-3，-2）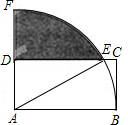
（2013•梅州）如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．
（2013•梅州）如图，已知抛物线y=2x2-2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．