题目内容
 (2013•梅州)如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(2013•梅州)如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P、N的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
分析:(1)在二次函数的解析式y=2x2-2中,令y=0,求出x=±1,得到AB=2,令x=0时,求出y=-2,得到OC=2,然后根据三角形的面积公式即可求出△ABC的面积;
(2)先将y=6代入y=2x2-2,求出x=±2,得到点M与点N的坐标,则MN=4,再由平行四边形的面积公式得到MN边上的高为2,则P点纵坐标为8或4.分两种情况讨论:①当P点纵坐标为8时,将y=8代入y=2x2-2,求出x的值,得到点P的坐标;②当P点纵坐标为4时,将y=4代入y=2x2-2,求出x的值,得到点P的坐标;
(3)由于∠QDB=∠BOC=90°,所以以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似时,分两种情况讨论:①OB与BD边是对应边,②OB与QD边是对应边两种情况,根据相似三角形对应边成比例列式计算求出QD的长度即可.
(2)先将y=6代入y=2x2-2,求出x=±2,得到点M与点N的坐标,则MN=4,再由平行四边形的面积公式得到MN边上的高为2,则P点纵坐标为8或4.分两种情况讨论:①当P点纵坐标为8时,将y=8代入y=2x2-2,求出x的值,得到点P的坐标;②当P点纵坐标为4时,将y=4代入y=2x2-2,求出x的值,得到点P的坐标;
(3)由于∠QDB=∠BOC=90°,所以以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似时,分两种情况讨论:①OB与BD边是对应边,②OB与QD边是对应边两种情况,根据相似三角形对应边成比例列式计算求出QD的长度即可.
解答:解:(1)∵y=2x2-2,
∴当y=0时,2x2-2=0,x=±1,
∴点A的坐标为(-1,0),点B的坐标为(1,0),AB=2,
又当x=0时,y=-2,
∴点C的坐标为(0,-2),OC=2,
∴S△ABC=
AB•OC=
×2×2=2;
(2)将y=6代入y=2x2-2,
得2x2-2=6,x=±2,
∴点M的坐标为(-2,6),点N的坐标为(2,6),MN=4.
∵平行四边形的面积为8,
∴MN边上的高为:8÷4=2,
∴P点纵坐标为6±2.
①当P点纵坐标为6+2=8时,2x2-2=8,x=±
,
∴点P的坐标为(
,8)或(-
,8);
②当P点纵坐标为6-2=4时,2x2-2=4,x=±
,
∴点P的坐标为(
,4)或(-
,4);
 (3)∵点B的坐标为(1,0),点C的坐标为(0,-2),
(3)∵点B的坐标为(1,0),点C的坐标为(0,-2),
∴OB=1,OC=2.
∵∠QDB=∠BOC=90°,
∴以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似时,分两种情况:
①OB与BD边是对应边时,△OBC∽△DBQ,
则
=
,即
=
,
解得DQ=2(m-1)=2m-2,
②OB与QD边是对应边时,△OBC∽△DQB,
则
=
,即
=
,
解得DQ=
.
综上所述,线段QD的长为2m-2或
.
∴当y=0时,2x2-2=0,x=±1,
∴点A的坐标为(-1,0),点B的坐标为(1,0),AB=2,
又当x=0时,y=-2,
∴点C的坐标为(0,-2),OC=2,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)将y=6代入y=2x2-2,
得2x2-2=6,x=±2,
∴点M的坐标为(-2,6),点N的坐标为(2,6),MN=4.
∵平行四边形的面积为8,
∴MN边上的高为:8÷4=2,
∴P点纵坐标为6±2.
①当P点纵坐标为6+2=8时,2x2-2=8,x=±
| 5 |
∴点P的坐标为(
| 5 |
| 5 |
②当P点纵坐标为6-2=4时,2x2-2=4,x=±
| 3 |
∴点P的坐标为(
| 3 |
| 3 |
 (3)∵点B的坐标为(1,0),点C的坐标为(0,-2),
(3)∵点B的坐标为(1,0),点C的坐标为(0,-2),∴OB=1,OC=2.
∵∠QDB=∠BOC=90°,
∴以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似时,分两种情况:
①OB与BD边是对应边时,△OBC∽△DBQ,
则
| OB |
| DB |
| OC |
| DQ |
| 1 |
| m-1 |
| 2 |
| DQ |
解得DQ=2(m-1)=2m-2,
②OB与QD边是对应边时,△OBC∽△DQB,
则
| OB |
| DQ |
| OC |
| DB |
| 1 |
| DQ |
| 2 |
| m-1 |
解得DQ=
| m-1 |
| 2 |
综上所述,线段QD的长为2m-2或
| m-1 |
| 2 |
点评:本题是对二次函数的综合考查,主要利用了二次函数图象上点的坐标特征,三角形、平行四边形的面积,相似三角形对应边成比例的性质,综合性较强,但难度不大,注意要分情况讨论求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
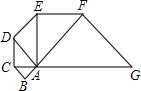 (2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是
(2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是 (2013•梅州)如图,在平面直角坐标系中,A(-2,2),B(-3,-2)
(2013•梅州)如图,在平面直角坐标系中,A(-2,2),B(-3,-2)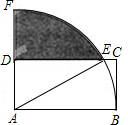 (2013•梅州)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(2013•梅州)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.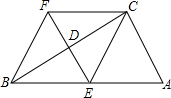 (2013•梅州)如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB与点E,且CF=AE,
(2013•梅州)如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB与点E,且CF=AE,