题目内容
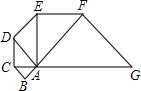 (2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是
(2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是(
)2013
| 2 |
(
)2013
.| 2 |
分析:设等腰直角三角形一个直角边为1,根据等腰直角三角形的斜边长为直角边长度的
倍,可以发现n个△,直角边是第(n-1)个△的斜边长,即可求出斜边长.
| 2 |
解答:解:设等腰直角三角形一个直角边为1,
等腰直角三角形的斜边长为直角边长度的
倍
第一个△(也就是Rt△ABC)的斜边长:1×
=
;
第二个△,直角边是第一个△的斜边长,所以它的斜边长:
×
=(
)2;
…
第n个△,直角边是第(n-1)个△的斜边长,其斜边长为:(
)n.
则第2013个等腰直角三角形的斜边长是:(
)2013.
故答案为:(
)2013.
等腰直角三角形的斜边长为直角边长度的
| 2 |
第一个△(也就是Rt△ABC)的斜边长:1×
| 2 |
| 2 |
第二个△,直角边是第一个△的斜边长,所以它的斜边长:
| 2 |
| 2 |
| 2 |
…
第n个△,直角边是第(n-1)个△的斜边长,其斜边长为:(
| 2 |
则第2013个等腰直角三角形的斜边长是:(
| 2 |
故答案为:(
| 2 |
点评:此题主要考查学生对等腰直角三角形的理解和掌握,解答此题的关键是通过认真分析,根据等腰直角三角形的斜边长为直角边长度的
倍,从中发现规律.此题有一定的拔高难度,属于中档题.
| 2 |

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 (2013•梅州)如图,在平面直角坐标系中,A(-2,2),B(-3,-2)
(2013•梅州)如图,在平面直角坐标系中,A(-2,2),B(-3,-2)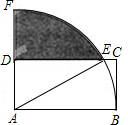 (2013•梅州)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(2013•梅州)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.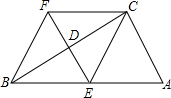 (2013•梅州)如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB与点E,且CF=AE,
(2013•梅州)如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB与点E,且CF=AE, (2013•梅州)如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(2013•梅州)如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.