��Ŀ����
����Ŀ�������κ���![]() ��
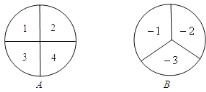
��![]() ��ͼ�����ԭ������ĶԳƣ����Ǿͳ�����һ����������һ�����������ĶԳƺ�����Ҳ�ƺ���
��ͼ�����ԭ������ĶԳƣ����Ǿͳ�����һ����������һ�����������ĶԳƺ�����Ҳ�ƺ���![]() ��
��![]() ��Ϊ���ĶԳƺ�����
��Ϊ���ĶԳƺ�����
![]() ����
����![]() �����ĶԳƺ�����
�����ĶԳƺ�����
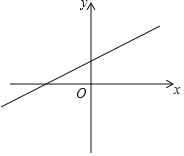
![]() ��ͼ����ƽ��ֱ������ϵxOy�У�E��F���������ֱ�Ϊ
��ͼ����ƽ��ֱ������ϵxOy�У�E��F���������ֱ�Ϊ![]() ��
��![]() �������
�����κ���![]() ��ͼ����E��ԭ��O������Ϊ
��ͼ����E��ԭ��O������Ϊ![]() ��֪����
��֪����![]() ��
��![]() ��Ϊ���ĶԳƺ�����
��Ϊ���ĶԳƺ�����
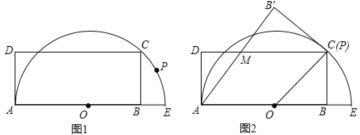
![]() ����ͼ���������κ���
����ͼ���������κ���![]() �Ķ���
�Ķ���![]() ��ͼ���߲���
��ͼ���߲���![]() ������������
������������![]() �Ĵ���ͼ��
�Ĵ���ͼ��
![]() ���ı���EPFQ�Ǿ���ʱ�������a��ֵ��
���ı���EPFQ�Ǿ���ʱ�������a��ֵ��
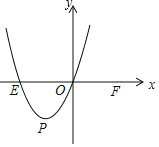
![]() ��֪���κ���
��֪���κ���![]() ��
��![]() ��Ϊ���ĶԳƺ�������
��Ϊ���ĶԳƺ�������![]() ��ͼ��
��ͼ��![]() �Ķ��㵱
�Ķ��㵱![]() ʱ�������ʽ
ʱ�������ʽ![]() �����ֵ��
�����ֵ��
���𰸡�![]() ��
��![]() ��ͼ��������
��ͼ��������![]() a��ֵΪ
a��ֵΪ![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ3��
�����ֵ�����ֵΪ3��
��������
![]() �����䷽���õ�
�����䷽���õ�![]() ����������ߵĶ�������Ϊ
����������ߵĶ�������Ϊ![]() ���������ĶԳƵ����ʵõ�
���������ĶԳƵ����ʵõ�![]() ����ԭ��ԳƵĵ������Ϊ
����ԭ��ԳƵĵ������Ϊ![]() ��Ȼ�����ö���ʽд������
��Ȼ�����ö���ʽд������![]() �����ĶԳƺ�������ʽ��
�����ĶԳƺ�������ʽ��
![]() ��P�����ԭ��ĶԳƵ�õ�q�㣬Ȼ����»�������ΪQ������ԭ���F��������ߣ�
��P�����ԭ��ĶԳƵ�õ�q�㣬Ȼ����»�������ΪQ������ԭ���F��������ߣ�
![]() ���þ��ε����ʵ�
���þ��ε����ʵ�![]() �������������ߵĶԳ��Եõ�
�������������ߵĶԳ��Եõ�![]() ������ж�
������ж�![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() ��H����ͼ����
��H����ͼ����![]() ��
��![]() ������
������![]() ���轻��ʽ
���轻��ʽ![]() ��Ȼ���P��������뼴�ɵõ�a��ֵ��
��Ȼ���P��������뼴�ɵõ�a��ֵ��
![]() ��
��![]() ��Ϊ����ʽ�õ�������
��Ϊ����ʽ�õ�������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() �����ù���ԭ��ԳƵĵ�����������õ�������
�����ù���ԭ��ԳƵĵ�����������õ�������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ���ٰ�
���ٰ�![]() ����
����![]() ��
��![]() ������
������![]() ��Ȼ�����ö��κ��������ʽ�����⣮
��Ȼ�����ö��κ��������ʽ�����⣮
![]() ��
��
![]() �������ߵĶ�������Ϊ
�������ߵĶ�������Ϊ![]() ��
��
![]() ��
��![]() ����ԭ��ԳƵĵ������Ϊ
����ԭ��ԳƵĵ������Ϊ![]() ��
��
![]() ����
����![]() �����ĶԳƺ���Ϊ
�����ĶԳƺ���Ϊ![]() ����
����![]() ��
��
![]() ��ͼ��
��ͼ��
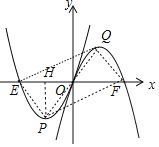
![]() �ı���EPFGΪ���Σ�
�ı���EPFGΪ���Σ�
![]() ��
��
��![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��H����ͼ��
��H����ͼ��
��![]() ��
��![]() ��
��
![]() ��
��
����κ���![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() �����
�����![]() �����
�����![]() ��
��
��a��ֵΪ![]() ��
��
![]() ��
��
![]() ������
������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��
![]() ������
������![]() �Ķ�����������
�Ķ�����������![]() �Ķ������ԭ��Գƣ�
�Ķ������ԭ��Գƣ�
![]() ������
������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��
��![]() ����
����![]() ��
��![]() �����
�����![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ3��
�����ֵ�����ֵΪ3��

����Ŀ��������20�����ˣ�ijһ�������������������ͳ�����±���
��������ĸ���(��) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
��������(��) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ.������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������