题目内容
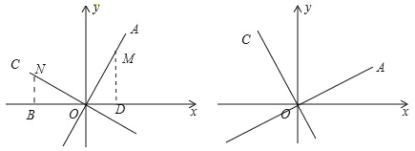
【题目】（1）问题提出：如图已知直线OA的解析式是y＝2x，OC⊥OA，求直线OC的函数解析式．
甲同学提出了他的想法：在直线y＝2x上取一点M，过M作x轴的垂线，垂足为D设点M的横坐标为m，则点M的纵坐标为2m．即OD＝m，MD＝2m，然后在OC上截取ON＝OM，过N作x轴的垂线垂足为B．则点N的坐标为 ，直线OC的解析式为 ．
（2）拓展：已知直线OA的解析式是y＝kx，OC⊥OA，求直线OC的函数解析式．
（3）应用：直接写出经过P（2，3），且垂直于直线y＝﹣
x+2的直线解析式 ．
【答案】（1）（﹣2m，m），y＝﹣
x（2）y＝﹣
x（3）y＝3x﹣3
【解析】
（1）设出点M的坐标，构造全等三角形，进而求出点N坐标，最后用待定系数法即可得出结论；
（2）同（1）的方法即可得出结论；
（3）先根据（2）求出直线的比例系数，最后将点P的坐标代入即可得出结论．
（1）在第一象限直线y＝2x上取一点M，过M作x轴的垂线，垂足为D，在第二象限OC上截取ON＝OM，过N作x轴的垂线，垂足为B．
∴∠ODM＝∠OBN＝90°，
∴∠DOM+∠DMO＝90°，
∵OA⊥OC，
∴∠DOM+∠BON＝90°，
∴∠DMO＝∠BON，
在△ODM和△NBO中，
，
∴△ODM≌△NBO（AAS），
∴DM＝OB，OD＝BN，
∵设点M的横坐标为m，则点M的纵坐标为2m．
∴OD＝m，MD＝2m，
∴OB＝2m，BN＝m，
∴N（﹣2m，m），
设直线OC的解析式为y＝kx，
∴﹣2mk＝m，
∴k＝﹣，
∴直线OC的解析式为y＝﹣x，
故答案为（﹣2m，m），y＝﹣x；
（2）当k＞0时，在第一象限直线y＝kx上取一点M，过M作x轴的垂线，垂足为D，在第二象限OC上截取ON＝OM，过N作x轴的垂线，垂足为B．
∴∠ODM＝∠OBN＝90°，
∴∠DOM+∠DMO＝90°，
∵OA⊥OC，
∴∠DOM+∠BON＝90°，
∴∠DMO＝∠BON，
在△ODM和△NBO中，，
∴△ODM≌△NBO（AAS），
∴DM＝OB，OD＝BN，
∵设点M的横坐标为m，则点M的纵坐标为km．
∴OD＝m，MD＝km，
∴OB＝km，BN＝m，
∴N（﹣km，m），
设直线OC的解析式为y＝k'x，
∴﹣2kmk'＝m，
∴k＝﹣
，
∴直线OC的解析式为y＝﹣x；
当k＜0时，同理可得，直线OC的解析式为y＝﹣
x；
即：直线OC的解析式为y＝﹣x；
（3）同（2）的方法得，直线y＝kx与直线y＝k'x垂直，可得kk'＝﹣1，
设过点P的直线解析式为y＝kx+b，
∵经过P（2，3），且垂直于直线y＝﹣
x+2，
∴k＝3，
∴过点P的直线解析式为y＝3x+b，
∴3×2+b＝3，
∴b＝﹣3，
∴过点P的直线解析式为y＝3x﹣3，
故答案为y＝3x﹣3．
