题目内容
【题目】在△ABC中,BC=3 ![]() ,AC=5,∠B=45°,对于下面四个结论:
,AC=5,∠B=45°,对于下面四个结论:
①∠C一定是钝角; ②△ABC的外接圆半径为3;③sinA= ![]() ;④△ABC外接圆的外切正六边形的边长是
;④△ABC外接圆的外切正六边形的边长是 ![]() .其中正确的个数是( )
.其中正确的个数是( )
A.1
B.2
C.3
D.4
【答案】C
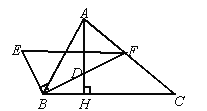
【解析】解:如图1,过C作CD⊥AB于D,过A作AE⊥BC于E,

∵∠B=45°,
∴△BDC是等腰直角三角形,
∵BC=3 ![]() ,
,
∴BD=CD=3,
由勾股定理得:AD= ![]() =
= ![]() =4,
=4,
∴sin∠BAC= ![]() =
= ![]() ,
,
所以③正确;
由S△ABC= ![]() ABCD=
ABCD= ![]() CBAE,
CBAE,
∴7×3=3 ![]() AE,
AE,
AE= ![]() =
= ![]() ,
,
在Rt△ABE中,
BE= ![]() =
= ![]() =
= ![]() >BC=3
>BC=3 ![]() =
= ![]() ,
,
∴∠ACB>90°,
即∠C一定是钝角;
所以①正确;
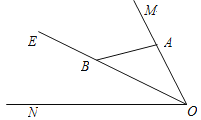
如图2,设△ABC的外接圆的圆心为O,连接OA、OC,
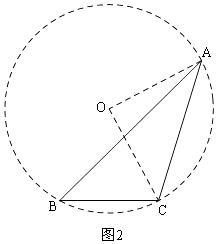
∵∠B=45°,
∴∠AOC=2∠B=90°,
∵OA=OC,
∴△AOC是等腰直角三角形,
∵AC=5,
∴OA= ![]() =
= ![]() ,
,
则△ABC的外接圆半径为 ![]() ;
;
所以②不正确;
如图3,此正六边形是△ABC的外接圆的外切正六边形,
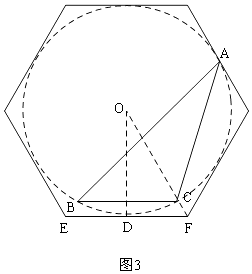
Rt△ODF中,由②得:OD= ![]() ,
,
由题意得:△OEF是等边三角形,
∴∠OFE=60°,
tan60°= ![]() =
= ![]() ,
,
∴EF=2DF= ![]() ,
,
则△ABC外接圆的外切正六边形的边长是 ![]() ,
,
所以④正确,
故本题正确的结论有:①③④;3个;
所以答案是:C.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握正多边形和圆(圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?